练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知P为正△ABC内的一点，∠APB=113°，∠APC=123°，求证：以AP、BP、CP为边构成一个三角形，并确定所构成的三角形各内角的度数.

     

    答案：
    解析：

    		如图，以点C为中心，将△APC逆时针旋转60°，A点移动到B点的位置，这时CP=CP1，∠PCP1=60°，AP=BP1，∠BP1C=∠APC=123°.

    由CP=CP1，∠PCP1=60°得△PP1C是等边三角形.

    所以：PP1=CP，∠CPP1=∠PP1C=60°

    这时△BPP1就是以BP、BP1、PP1.

    即：BP、AP、PC为三边构成的三角形.

    ∠BP1P=∠BP1C－∠PP1C=∠APC－60°=63°

    ∠BPC=360°－113°－123°=124°

    所以∠BPP1=∠BPC－∠P1PC=124°－60°=64°

    ∠PBP1=180°－63°－64°=53°

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网已知：如图，边长为a的正△ABC内有一边长为b的内接正△DEF，则△AEF的内切圆半径为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•新华区一模）已知：等边△ABC的面积为S，Dn，En，Fn（n为正整数0分别是AB，BC，CA边上的点，连接DnEn，EnFn，FnDn，可得△DnEnFn．
    如图1，当AD1=BE1=CF1=
    1
    2
    AB时，我们容易得到△D1E1F1是等边三角形，且S△AD1F1=S△D1E1F1=
    1
    4
    S．
    探究论证：
    （1）如图2，当AD2=BE2=CF2=
    1
    3
    AB时，
    ①△D2E2F2是
    等边
    等边
    三角形（填写“等腰”或“等边”或“不等边”）；
    ②S△AD2F2=
    2
    9
    S
    2
    9
    S
    ；S△D2E2F2=
    1
    3
    S
    1
    3
    S
    （用含S的代数式表示）；
    ③请说明以上结论的正确性．
    猜想发现：
    （2）如图3，当ADn=BEn=CFn=
    1
    n+1
    AB时，
    ①△DnEnFn是
    等边
    等边
    三角形（填写“等腰”或“等边”或“不等边”）；
    ②S△ADnFn=
    n
    (n+1)2
    S
    n
    (n+1)2
    S
    ；S△DnEnFn=
    n2-n+1
    (n+1)2
    S
    n2-n+1
    (n+1)2
    S
    （用含S的代数式表示）．
    实际应用：
    （3）学校有一块面积为49m2的等边△ABC空地，按如图4所示分割，其中AD6=BE6=CF6=
    1
    7
    AB，计划在△D6E6F6内栽种花卉，其余地方铺草坪，则栽种花卉（即阴影部分）的面积为多少m2？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    我们定义：“四个顶点都在三角形边上的正方形是三角形的内接正方形”．
    已知：在Rt△ABC中，∠C=90°，AC=6，BC=3．
    （1）如图1，四边形CDEF是△ABC的内接正方形，则正方形CDEF的边长a1是
    2
    2
    ；
    （2）如图2，四边形DGHI是（1）中△EDA的内接正方形，则第2个正方形DGHI的边长a2=
    4
    3
    4
    3
    ；继续在图2中的△HGA中按上述方法作第3个内接正方形；…以此类推，则第n个内接正方形的边长an=
    2n
    3n-1
    2n
    3n-1
    ．（n为正整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    我们定义：“四个顶点都在三角形边上的正方形是三角形的内接正方形” ．

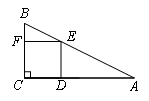
    已知：在Rt△ABC中，∠C=90°，AC=6，BC=3．

    （1）如图，四边形CDEF是△ABC的内接正方形，则正方形CDEF的边长a1是            ；

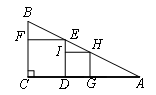
    （2）如图，四边形DGHI是（1）中△EDA的内接正方形，则第2个正方形DGHI的边长a2=              ；继续在图2中的△HGA中按上述方法作第3个内接正方形；…以此类推，则第n个内接正方形的边长an=              ．（n为正整数）

     

    查看答案和解析>>

    同步练习册答案