
 )、D(0,3
)、D(0,3 ),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.
 ),
), );
);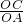 =
=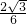 =
= ,
, ),
),
 ,
, =3,
=3, );
); ),②30,③(3,3
),②30,③(3,3 );
);
 (3-m)=
(3-m)= AM=
AM= AN=
AN= ,
, (3-m)=
(3-m)= ,
, ,
,
 ,
, =
= =3,GQ=
=3,GQ= =
= ,
, AN=1.5,
AN=1.5,
 ,
, (3+x),
(3+x), (EF+OQ)•OC=
(EF+OQ)•OC= (3+x),
(3+x),
 AH•AQ=
AH•AQ= (3+x)-
(3+x)- (x-3)2,
(x-3)2,
 x,
x, x,
x, (BE+OA)•OC=
(BE+OA)•OC= (12-
(12- x),
x),
 OA•AH=
OA•AH= .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
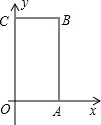 如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).
如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 |
| 9 |
| 4 |
| 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 |
| 9 |

| 4 |
| 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,矩形OABC中,OA=2,OC=1,把矩形OABC放在数轴上,O在原点,OA在正半轴上,把矩形的对角线OB绕着原点O顺时针旋转到数轴上,点B的对应点为B′,则点B′表示的实数是( )
如图,矩形OABC中,OA=2,OC=1,把矩形OABC放在数轴上,O在原点,OA在正半轴上,把矩形的对角线OB绕着原点O顺时针旋转到数轴上,点B的对应点为B′,则点B′表示的实数是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com