
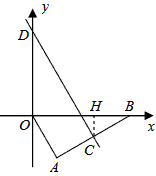
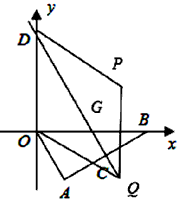
 ,边AB的垂直平分线CD分别与AB、x轴、y轴交于点C、G、D。
,边AB的垂直平分线CD分别与AB、x轴、y轴交于点C、G、D。
| 解:(1)∵DC是AB垂直平分线,OA垂直AB, ∴G点为OB的中点 ∵ 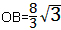 ∴ 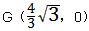 。 。 |
|
| (2)过点C作CH⊥x轴于点H 在Rt△ABO中,∠ABO=30°, 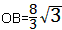 ∴ 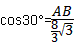 即 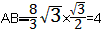 又∵CD垂直平分AB ∴BC=2, 在Rt△CBH中,CH= 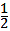 BC=1, BC=1,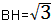 ∴ 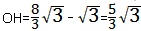 ∴ 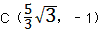 ∵∠DGO=60° ∴ 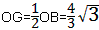 ∴ 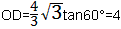 ∴D(0,4) 设直线CD的解析式为:y=kx+b 则 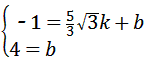 解得 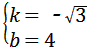 ∴ 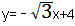 。 。 |
 |
| (3)存在点Q、P,使得以O、D、P、Q为顶点的四边形是菱形 ①如图,当OD=DQ=QP=OP=4时,四边形DOPQ为菱形 设QP交x轴于点E,在Rt△OEP中,OP=4,∠OPE=30° ∴OE=2, 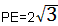 ∴ 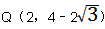 |
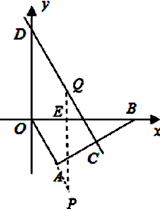 |
| ②如图,当OD=DQ=QP=OP=4时,四边形DOPQ为菱形, 延长QP交x轴于点F,在Rt△POF中,OP=4,∠FPO=30° ∴ 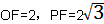 ∴ 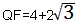 ∴ 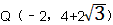 |
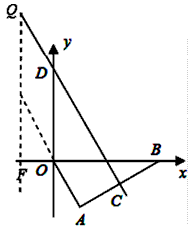 |
③如图,当PD=DQ=QO=OP=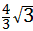 时,四边形DOPQ为菱形, 时,四边形DOPQ为菱形,在Rt△DQM中,∠MDQ=30°, ∴ 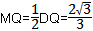 ∴ 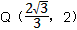 。 。 |
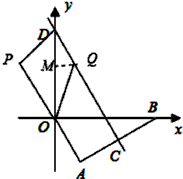 |
| ④如图,当OD=DQ=QP=OP=4时,四边形DOPQ为菱形, 设PQ交x轴于点N,此时∠OQP=∠ODQ=30° 在Rt△ONQ中, 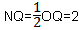 ∴ 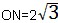 ∴ 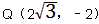 综上所述,满足条件的点Q共有四点: 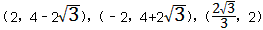 ,( ,(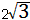 ,-2)。 ,-2)。 |
 |


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
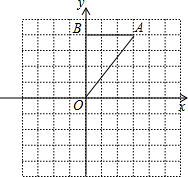 如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).
如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).查看答案和解析>>
科目:初中数学 来源: 题型:
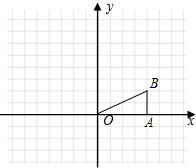 OA1B1.
OA1B1.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△OAB中,∠OBA=90°,OB=AB=4,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
如图,在Rt△OAB中,∠OBA=90°,OB=AB=4,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
(2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com