
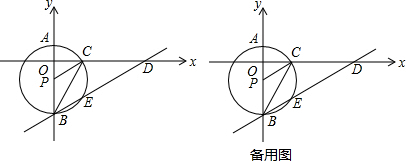
分析 (1)在Rt△OPC中,根据OC=$\sqrt{P{C}^{2}-O{P}^{2}}$计算即可.
(2)只要证明∠OCP=30°即可解决问题.
(3)①$\frac{BE}{OP}$是定值.由△CPO∽△PBH,推出$\frac{OP}{BH}$=$\frac{PC}{PB}$,可得$\frac{-t}{BH}$=$\frac{4}{4}$,推出BH=-t,BE=-2t,由此即可解决问题.②由PC∥BD,推出$\frac{PC}{BD}$=$\frac{OP}{OB}$,可得$\frac{4}{BD}$=$\frac{-t}{-t+4}$,
推出BD=$\frac{4(t-4)}{t}$,DE=BD-BE=$\frac{4(t-4)}{t}$-(-2t)=$\frac{4(t-4)}{t}$+2t,推出BE•DE=-2t[$\frac{4(t-4)}{t}$+2t]=-4(t+1)2+36,由此即可解决问题.
解答 解:(1)如图1中,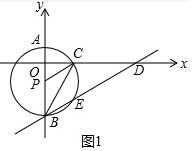
∵P(0,-3),
∴OP=3,PC=4,
在Rt△OPC中,OC=$\sqrt{P{C}^{2}-O{P}^{2}}$=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$.
(2)如图2中,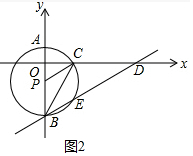
∵PB=PC,
∴∠PCB=∠PBC,
∵△PBC与△CBD相似,
∴∠CBD=∠CDB=∠PCB=∠PBC,
∵PC∥BD,
∴∠OCP=∠CDB,
∴∠OCP=∠PCB=∠PBC,
∴∠OCP=30°,
∵PC=4,
∴OP=$\frac{1}{2}$PC=2,
∴t=-2.
(3)①$\frac{BE}{OP}$是定值.理由如下:
如图3中,作PH⊥BD于H.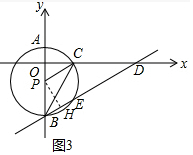
∵PH⊥BE,
∴BH=HE,
∵PC∥BD,
∴PH⊥PC,
∴∠CPH=90°,
易证△CPO∽△PBH,
∴$\frac{OP}{BH}$=$\frac{PC}{PB}$,
∴$\frac{-t}{BH}$=$\frac{4}{4}$,
∴BH=-t,
∴BE=-2t,
∴$\frac{BE}{OP}$=$\frac{-2t}{-t}$=2.
∴$\frac{BE}{OP}$是定值.
②∵PC∥BD,
∴$\frac{PC}{BD}$=$\frac{OP}{OB}$,
∴$\frac{4}{BD}$=$\frac{-t}{-t+4}$,
∴BD=$\frac{4(t-4)}{t}$,
∴DE=BD-BE=$\frac{4(t-4)}{t}$-(-2t)=$\frac{4(t-4)}{t}$+2t,
∴BE•DE=-2t[$\frac{4(t-4)}{t}$+2t]=-4(t+1)2+36.
∵-4<0,
∴t=-1时,BE•DE定值最大,最大值为36.
点评 本题考查圆综合题、二次函数的性质、平行线分线段成比例定理、相似三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线构造相似三角形解决问题,学会用方程的思想思考问题,属于中考压轴题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,Rt△CEF中,∠ECF=90°,面积为200,则BE的值为12.
如图,正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,Rt△CEF中,∠ECF=90°,面积为200,则BE的值为12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
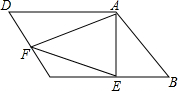 已知:在平行四边形ABCD中,AE⊥BC,垂足为E,点F为CD的中点,连接AF,EE.
已知:在平行四边形ABCD中,AE⊥BC,垂足为E,点F为CD的中点,连接AF,EE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -3 | -2 | -1 | $-\frac{1}{2}$ | $-\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | $\frac{25}{6}$ | $\frac{3}{2}$ | $-\frac{1}{2}$ | $-\frac{15}{8}$ | -$\frac{53}{18}$ | $\frac{55}{18}$ | $\frac{17}{8}$ | $\frac{3}{2}$ | $\frac{5}{2}$ | m | … |

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0≤m≤1.5 | B. | m≥1.5 | C. | 0≤m≤2.5 | D. | 0<m≤1.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com