
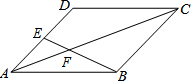
 如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F,则
如图,在?ABCD中,点E为AD的中点,连接BE,交AC于点F,则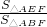 =________.
=________.
 ,根据平行四边形的性质可知S△ABC=
,根据平行四边形的性质可知S△ABC= S?ABCD=
S?ABCD= ,即S△BCF+a=
,即S△BCF+a= ,再由相似三角形的判定定理可得出△AEF∽△BCF,故可得出S△AEF:S△BCF=1:4,由此可用s表示出a的值,进而得出结论.
,再由相似三角形的判定定理可得出△AEF∽△BCF,故可得出S△AEF:S△BCF=1:4,由此可用s表示出a的值,进而得出结论. ,
, S?ABCD=
S?ABCD= ,即S△BCF+a=
,即S△BCF+a= ,
,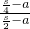 =
= ,解得a=
,解得a= ,即S△ABF=
,即S△ABF= ,
, -a=
-a= -
- =
= ,
,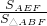 =
=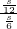 =
= .
. .
.

科目:初中数学 来源: 题型:
 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=| 29 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com