
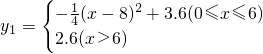 ;每年投资t万元进行B种饼干的广告,其销售量将是原来的y2倍,且
;每年投资t万元进行B种饼干的广告,其销售量将是原来的y2倍,且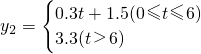 .该厂实行以销定产.
.该厂实行以销定产. (x-8)2+3.6]+3[0.3(10-x)+1.5],
(x-8)2+3.6]+3[0.3(10-x)+1.5], x2+8x-32+7.2+9-0.9x+4.5,
x2+8x-32+7.2+9-0.9x+4.5, x2+7.1x-11.3,
x2+7.1x-11.3, =-
=-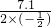 =7.1,
=7.1, <0,
<0, ×62+7.1×6-11.3=13.3万千克,
×62+7.1×6-11.3=13.3万千克, (6-8)2+3.6]=5.2万千克,
(6-8)2+3.6]=5.2万千克,

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com