
(1)证明:连接BE,
∵点P是△ABC的内心,
∴∠BAD=∠CAD.
又∵FG切⊙O于E,
∴∠BEF=∠BAD.
又∵∠DBE=∠CAD,
∴∠BEF=∠DBE.
∴BC∥FG.
(2)解:连接BP,
则∠ABP=∠CBP.
∵∠BPE=∠BAP+∠ABP=∠PBC+∠EBD,
∴∠BPE=∠PBE.
∴BE=PE.
在△ABE和△BDE中,
∠BAE=∠EBD,∠BED=∠AEB,
∴△ABE∽△BDE.
∴
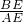
=

.
∴BE
2=AE•DE.
∴PE
2=AE•DE.
(3)解:∵FE
2=FB•FA=FB(FB+AB),
而FE=AB,
∴AB
2=3(3+AB).
设AB=x,则x
2-3x-9=0,
解之得x=

.
∴AB=

(取正值).
由(1)在△AFG中,BC∥FG,
∴

.
∴AC=

=

×

=1+

.
∴AG=AC+CG=3+

.
分析:(1)连接BE.构造了一对内错角,根据三角形的内心是三角形三条角平分线的交点,结合弦切角定理和圆周角定理的推论即可证明内错角相等,从而证明平行;
(2)连接BP.根据三角形的内心的概念以及三角形的外角的性质,可以得到一个等腰三角形,即BE=PE,根据相似三角形的性质可以把要找的线段之间的关系联系起来;
(3)结合(2)的结论首先求得AB的长,再根据平行线分线段成比例定理求得AG的长.
点评:综合运用了三角形的内心的概念、弦切角定理、圆周角定理的推论、相似三角形的判定和性质.

 于点D,交⊙O于点E,经过点E作⊙O的切线分别交AB、AC延长线于点F、G.
于点D,交⊙O于点E,经过点E作⊙O的切线分别交AB、AC延长线于点F、G. (1)证明:连接BE,
(1)证明:连接BE,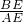 =
= .
. .
. (取正值).
(取正值). .
. =
= ×
× =1+
=1+ .
. .
.



