
 如图,将边长为4cm的正方形ABCD绕顶点C顺时针方向旋转30°,得到正方形EFCG,且EF交AD于点H.
如图,将边长为4cm的正方形ABCD绕顶点C顺时针方向旋转30°,得到正方形EFCG,且EF交AD于点H.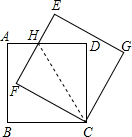 (1)证明:连接CH,
(1)证明:连接CH, ,
, ∠FCD=30°,
∠FCD=30°, =
= ,
, ×FH×CF=
×FH×CF= ×
× ×4=
×4= ,
,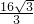 .
.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2011•黔西南州)如图,将边长为4cm的正方形ABCD绕顶点C顺时针方向旋转30°,得到正方形EFCG,且EF交AD于点H.
(2011•黔西南州)如图,将边长为4cm的正方形ABCD绕顶点C顺时针方向旋转30°,得到正方形EFCG,且EF交AD于点H.查看答案和解析>>
科目:初中数学 来源: 题型:
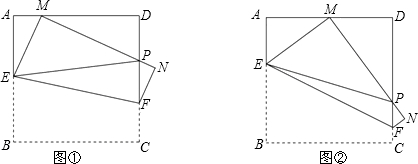
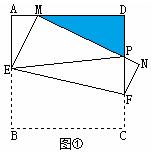
(本题满分14分)如图①,将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点 M处,点C落在点N处,MN与CD交于点P, 连接EP.
⑴如图②,若M为AD边的中点,①△AEM的周长=____ _cm;②求证:EP=AE+DP;

⑵随着落点M在AD边上取遍所有的位置(点M不与A、D重合),△PDM的周长是否发生变化?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省盐城市九年级第一学期期中考试数学卷 题型:解答题
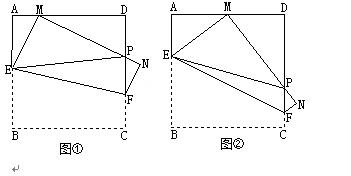
(本题满分14分)如图①,将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点 M处,点C落在点N处,MN与CD交于点P, 连接EP.
⑴如图②,若M为AD边的中点,①△AEM的周长=____ _cm;②求证:EP=AE+DP;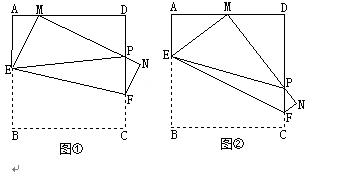
⑵随着落点M在AD边上取遍所有的位置(点M不与A、D重合),△PDM的周长是否发生变化?请说明理由.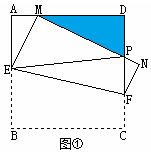
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com