解:(1)把x=-1,y=0代入y=x
2-2x+c得:1+2+c=0
∴c=-3
∴y=x
2-2x-3=y=(x-1)
2-4
∴顶点坐标为(1,-4);
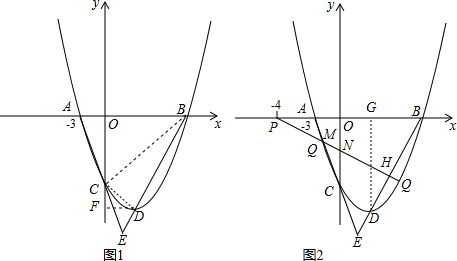
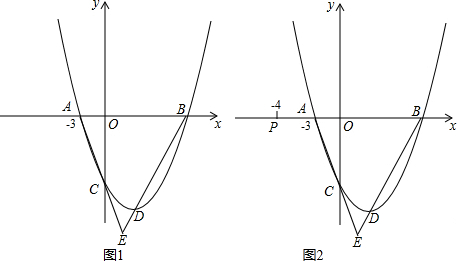
(2)如图1,连接CD、CB,过点D作DF⊥y轴于点F,
由x
2-2x-3=0得x=-1或x=3
∴B(3,0)
当x=0时,y=x
2-2x-3=-3
∴C(0,-3)
∴OB=OC=3
∵∠BOC=90°,
∴∠OCB=45°,
BC=3

又∵DF=CF=1,∠CFD=90°,
∴∠FCD=45°,CD=

,
∴∠BCD=180°-∠OCB-∠FCD=90°.
∴∠BCD=∠COA
又∵
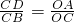
∴△DCB∽△AOC,
∴∠CBD=∠OCA
又∵∠ACB=∠CBD+∠E=∠OCA+∠OCB
∴∠E=∠OCB=45°,
(3)如图2,设直线PQ交y轴于N点,交BD于H点,作DG⊥x轴于G点
∵∠PMA=45°,
∴∠EMH=45°,
∴∠MHE=90°,
∴∠PHB=90°,
∴∠DBG+∠OPN=90°
又∴∠ONP+∠OPN=90°,
∴∠DBG=∠ONP
又∵∠DGB=∠PON=90°,
∴△DGB=∠PON=90°,
∴△DGB∽△PON
∴
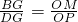
即:

=

∴ON=2,
∴N(0,-2)
设直线PQ的解析式为y=kx+b
则
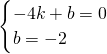
解得:
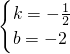
∴y=-

x-2
设Q(m,n)且n<0,
∴n=-

m-2
又∵Q(m,n)在y=x
2-2x-3上,
∴n=m
2-2m-3
∴-

m-2=m
2-2m-3
解得:m=2或m=-

∴n=-3或n=-

∴点Q的坐标为(2,-3)或(-

,-

).
分析:(1)将点A的坐标代入到抛物线的解析式求得c值,然后配方后即可确定顶点D的坐标;
(2)连接CD、CB,过点D作DF⊥y轴于点F,首先求得点C的坐标,然后证得△DCB∽△AOC得到∠CBD=∠OCA,根据∠ACB=∠CBD+∠E=∠OCA+∠OCB,得到∠E=∠OCB=45°;
(3)设直线PQ交y轴于N点,交BD于H点,作DG⊥x轴于G点,增大△DGB∽△PON后利用相似三角形的性质求得ON的长,从而求得点N的坐标,进而求得直线PQ的解析式,
设Q(m,n),根据点Q在y=x
2-2x-3上,得到-

m-2=m
2-2m-3,求得m、n的值后即可求得点Q的坐标.
点评:本题考查了二次函数的综合知识,难度较大,题目中渗透了许多的知识点,特别是二次函数与相似三角形的结合,更是一个难点,同时也是中考中的常考题型之一.

 解:(1)把x=-1,y=0代入y=x2-2x+c得:1+2+c=0
解:(1)把x=-1,y=0代入y=x2-2x+c得:1+2+c=0
 ,
,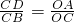
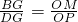
 =
=
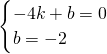
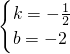
 x-2
x-2 m-2
m-2 m-2=m2-2m-3
m-2=m2-2m-3

 ,-
,- ).
). m-2=m2-2m-3,求得m、n的值后即可求得点Q的坐标.
m-2=m2-2m-3,求得m、n的值后即可求得点Q的坐标.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.