
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:北京市顺义区2017-2018学年度第一学期期末教学质量检测八年级数学试卷 题型:解答题
已知: 如图,点B、A、D、E在同一直线上,BD=AE,BC∥EF,∠C=∠F.求证:AC=DF.
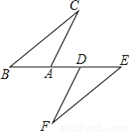
查看答案和解析>>
科目:初中数学 来源:北京市西城区2017-2018学年度第一学期期末考试七年级数学试卷 题型:填空题
一个有理数x满足:x<0且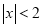 ,写出一个满足条件的有理数x的值:x=______.
,写出一个满足条件的有理数x的值:x=______.
查看答案和解析>>
科目:初中数学 来源:上海市普陀区(五四制)2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
计算: 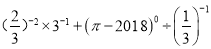 .
.
查看答案和解析>>
科目:初中数学 来源:上海市普陀区(五四制)2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
在下列图形中:等腰三角形、等边三角形、正方形、正五边形、平行四边形,等腰梯形,其中有_________个旋转对称图形.
4 【解析】等腰三角形、等腰梯形是轴对称图形; 等边三角形、正方形、正五边形既是轴对称图形又是是旋转对称图形; 平行四边形是旋转对称图形; ∴有4个旋转对称图形.查看答案和解析>>
科目:初中数学 来源:上海市普陀区(五四制)2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
下列说法中,正确的是( )
A. 将一个图形先向左平移3厘米,再向下平移5厘米,那么平移的距离是8厘米
B. 将一个图形绕任意一点旋转360°后,能与初始图形重合
C. 等边三角形至少旋转60°能与本身重合
D. 面积相等的两个三角形一定关于某条直线成轴对称
B 【解析】A.平移的距离是厘米,故不正确; B. 将一个图形绕任意一点旋转360°后,回到了原来的位置,所以能与初始图形重合,故正确; C. 等边三角形至少旋转120°能与本身重合,故不正确; D.面积相等的两个三角形不一定关于某条直线成轴对称,关于某条直线成轴对称两个三角形的面积一定相等,故不正确. 故选B.查看答案和解析>>
科目:初中数学 来源:辽宁省葫芦岛市建昌县2017-2018学年七年级上学期期末测评数学试卷 题型:解答题
2017年国庆节放假八天,高速公路免费通行,各地风景区游人如织.其中闻名于世的北京故宫在10月1日的游客人数就已经达到了7万人,接下来的七天中,每天的游客人数变化(单位:万人)如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):

(1) 10月3日的人数为____万人;
(2)这八天,游客人数最多的是10月____日,达到____万人;游客人数最少的是10月____日,为____万人;
(3)这8天参观故宫的总人数约为 万人(结果精确到万位)
(4)如果你们一家人打算在下一个国庆节参观故宫,请你对你们的出行日期提一个建议.
(1)7.8;(2)4,7.9,8,5.2;(3)55;(4)尽量把参观日期向后安排(言之有理即可) 【解析】试题分析:(1)根据题意计算出10月2日的人数再加上0.6即可; (2)分别计算出每天的人数,即可作出判断; (3)根据(2)把8天的人数相加即可; (4)答案不唯一,只要合理即可. 试题解析:(1)2日的人数为:7+0.6=7.6万人, 3日的人数为:...查看答案和解析>>
科目:初中数学 来源:辽宁省葫芦岛市建昌县2017-2018学年七年级上学期期末测评数学试卷 题型:单选题
下列方程中,是一元一次方程的是( )
A. 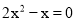 B.
B. 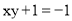 C.
C. 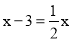 D.
D. 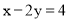
查看答案和解析>>
科目:初中数学 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:填空题
在△ABC中,∠C=90°,AB=10,BC=8,则cos A=________.
【解析】先利用勾股定理求出AC的长,再利用锐角三角函数关系得出cosA=,即可得出答案. 【解析】 如图所示, ∵∠C=90°,AB=10,BC=8, 由勾股定理得,AC=, ∴cosA= ==. 故答案为: .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com