(1)证明:∵∠ACB=90°,CB=CA=

,
∴∠A=∠B=

=45°.
∵∠ECF=45°,
∴∠B=∠ECF,
又∵∠CEF=∠B+∠BCE=45°+∠BCE,
∠BCF=∠ECF+∠BCE=45°+∠BCE,
∴∠CEF=∠BCF.
∴△BCF∽△AEC.
∴
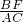
=

,
∴BF•AE=AC•BC=

•

=2;
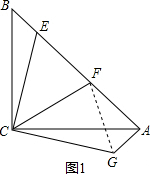
(2)解:BE、EF、FA三条线段所组成的三角形是直角三角形.
(解法一)如图1,将CE绕点C顺时针旋转90°得到CG,连结GA,GF,
∵∠BCE+∠ECA=∠ACG+∠ECA=90°
∴∠BCE=∠ACG.
∵在△BCE与△ACG中,
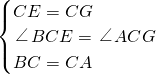
,
∴△BCE≌△ACG(SAS),
∴∠B=∠CAG=45°,BE=AG,
∴∠FAG=∠FAC+∠CAG=90°.
在Rt△FAG中,∠FAG=90°,
∴FG
2=AG
2+AF
2=BE
2+AF
2.
又∵∠ECF=45°,
∴∠FCG=∠ECG-∠ECF=45°=∠ECF.
∵在△BCF与△GCF中,
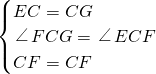
,
∴△ECF≌△GCF(SAS).
∴EF=GF,
∴EF
2=BE
2+AF
2.
∴BE、EF、FA三条线段所组成的三角形是直角三角形.
(解法二)如图,过A作AG⊥AF,使得AG=BE,连结GF,
∴∠CAG=∠BAG-∠BAC=45°=∠B.
∵在△BCE与△ACG中,
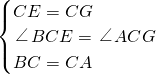
,
∴△BCE≌△ACG(SAS).
∴CE=CG,∠BCE=∠ACG.
∵∠ECG=∠ACG+∠ECA=∠BCE+∠ECA=90°,
∴∠FCG=∠ECG-∠FCG=45°=∠ECF.
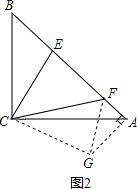
∵在△BCF与△GCF中,
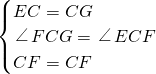
∴△ECF≌△GCF(SAS).
∴EF=GF,
在Rt△FAG中,∠FAG=90°,
∴FG
2=AG
2+AF
2=BE
2+AF
2.
∴EF
2=BE
2+AF
2.
∴BE、EF、FA三条线段所组成的三角形是直角三角形.
(解法三)∵CB=CA=

,∠ACB=90°,
∴
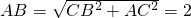
.
∴BE+EF+FA=2.
设BE=a,EF=b,FA=c,
则a+b+c=2.
∴(a+b+c)
2=4,
即a
2+b
2+c
2+2ab+2bc+2ac=4.①
又∵BF•AE=2,
∴(a+b)(b+c)=2,即ab+ac+b
2+bc=2.②
①-②×2得:a
2+c
2-b
2=0,
即a
2+c
2=b
2,EF
2=BE
2+AF
2.
∴BE、EF、FA三条线段所组成的三角形是直角三角形.
分析:(1)先根据等腰直角三角形的性质求出∠A与∠B的度数,再根据∠ECF=45°,可知∠B=∠ECF,根据等量代换可得出∠CEF=∠BCF,故可得出△BCF∽△AEC,根据相似三角形的对应边成比例即可得出结论;
(2)将CE绕点C顺时针旋转90°得到CG,连结GA,GF,先由全等三角形的判定定理得出△BCE≌△ACG,根据全等三角形的性质可得出△FAG中,∠FAG=90°,由勾股定理可知FG
2=AG
2+AF
2=BE
2+AF
2.故可得出∠FCG=∠ECG-∠ECF=45°=∠ECF,根据全等三角形的判定定理可知△BCF≌△GCF,故可得出EF=GF,故EF
2=BE
2+AF
2,由此可得出结论.
点评:本题考查的是全等三角形的判定与性质,涉及到勾股定理的逆定理、图形旋转不变性的性质等知识,难度适中.

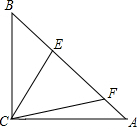 如图,在△ABC中,∠ACB=90°,CB=CA=
如图,在△ABC中,∠ACB=90°,CB=CA= ,点E、F在线段AB上(不与端点A、B重合),且∠ECF=45°.
,点E、F在线段AB上(不与端点A、B重合),且∠ECF=45°. ,
, =45°.
=45°.
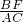 =
= ,
, •
• =2;
=2;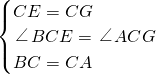 ,
,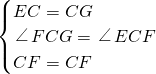 ,
,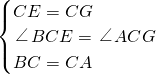 ,
,
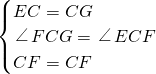
 ,∠ACB=90°,
,∠ACB=90°,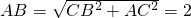 .
.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为