
 已知∠α,请用尺规作出∠AOB=∠α.(只保留作图痕迹,但不用写作法)
已知∠α,请用尺规作出∠AOB=∠α.(只保留作图痕迹,但不用写作法)科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
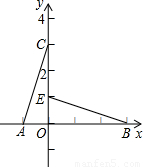
 已知:△AOC如图A(-1,0)、C(0,3),把△AOC 以O点为旋转中心顺时针方向旋转
已知:△AOC如图A(-1,0)、C(0,3),把△AOC 以O点为旋转中心顺时针方向旋转查看答案和解析>>
科目:初中数学 来源: 题型:
 的⊙
的⊙ ,对于任意点
,对于任意点 ,在射线
,在射线 上取一点
上取一点 ,使得
,使得 ·
· =
= ,这种把点
,这种把点 变为点
变为点 的变换叫做反演变换,点
的变换叫做反演变换,点 与点
与点 叫做互为反演点,⊙
叫做互为反演点,⊙ 称为基圆.
称为基圆.
 内有不同的两点
内有不同的两点 、
、 ,它们的反演点分别是
,它们的反演点分别是 、
、 ,则与∠
,则与∠ 一定相等的角是( ▲ )
一定相等的角是( ▲ )A.∠ | B.∠ | C.∠ | D.∠ |
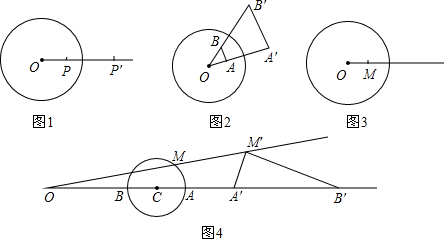
 内有一点
内有一点 ,请用尺规作图画出点
,请用尺规作图画出点 的反演点
的反演点 ;(保留画图痕迹,不必写画法).
;(保留画图痕迹,不必写画法). 的半径为
的半径为 ,另一个半径为
,另一个半径为 的⊙
的⊙ ,作射线
,作射线 交⊙
交⊙ 于点
于点 、
、 ,点
,点 、
、 关于⊙
关于⊙ 的反演点分别是
的反演点分别是 、
、 ,点
,点 为⊙
为⊙ 上另一点,关于⊙
上另一点,关于⊙ 的反演点为
的反演点为 .求证:∠
.求证:∠ =90°.
=90°.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年辽宁省盘锦市四完中九年级(上)第四次月考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com