
“2014年至2016年,中国同‘一带一路’沿线国家贸易总额超过3万亿美元”.将数据3万亿美元用科学记数法表示为( )
A.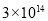 美元 B.
美元 B.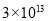 美元 C.
美元 C. 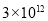 美元 D.
美元 D.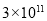 美元
美元
科目:初中数学 来源:2017年初中毕业升学考试(贵州毕节卷)数学(解析版) 题型:填空题
观察下列运算过程:
计算:1+2+22+…+210.
【解析】
设S=1+2+22+…+210,①
①×2得
2S=2+22+23+…+211,②?
②﹣①得
S=211﹣1.
所以,1+2+22+…+210=211﹣1
运用上面的计算方法计算:1+3+32+…+32017= .
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(山东泰安卷)数学(解析版) 题型:选择题
某班学生积极参加爱心活动,该班50名学生的捐款统计情况如下表:
金额/元 | 5 | 10 | 20 | 50 | 100 |
人数 | 4 | 16 | 15 | 9 | 6 |
则他们捐款金额的中位数和平均数分别是( )
A.10,20.6 B.20,20.6 C.10,30.6 D.20,30.6
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(山东青岛卷)数学(解析版) 题型:解答题
数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题。下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.
探究一:求不等式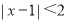 的解集
的解集
(1)探究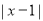 的几何意义
的几何意义
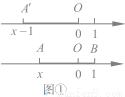
如图①,在以O为原点的数轴上,设点A'对应点的数为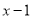 ,由绝对值的定义可知,点A'与O的距离为
,由绝对值的定义可知,点A'与O的距离为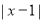 ,
,
可记为:A'O=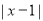 。将线段A'O向右平移一个单位,得到线段AB,,此时点A对应的数为
。将线段A'O向右平移一个单位,得到线段AB,,此时点A对应的数为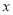 ,点B的对应数是1,
,点B的对应数是1,
因为AB= A'O,所以AB=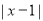 。
。
因此,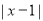 的几何意义可以理解为数轴上
的几何意义可以理解为数轴上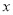 所对应的点A与1所对应的点B之间的距离AB。
所对应的点A与1所对应的点B之间的距离AB。
(2)求方程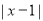 =2的解
=2的解
因为数轴上3与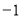 所对应的点与1所对应的点之间的距离都为2,所以方程的解为
所对应的点与1所对应的点之间的距离都为2,所以方程的解为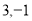
(3)求不等式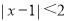 的解集
的解集
因为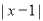 表示数轴上
表示数轴上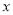 所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点所对应的数
所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点所对应的数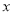 的范围。
的范围。
请在图②的数轴上表示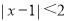 的解集,并写出这个解集
的解集,并写出这个解集
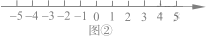
探究二:探究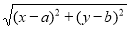 的几何意义
的几何意义
(1)探究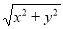 的几何意义
的几何意义
如图③,在直角坐标系中,设点M的坐标为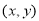 ,过M作MP⊥x轴于P,作MQ⊥y轴于Q,则点P点坐标(
,过M作MP⊥x轴于P,作MQ⊥y轴于Q,则点P点坐标(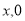 ),Q点坐标(
),Q点坐标(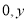 ),|OP|=
),|OP|=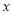 ,|OQ|=
,|OQ|=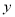 ,
,
在Rt△OPM中,PM=OQ=y,则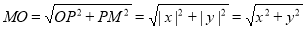
因此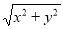 的几何意义可以理解为点M
的几何意义可以理解为点M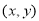 与原点O(0,0)之间的距离OM
与原点O(0,0)之间的距离OM
(2)探究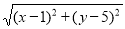 的几何意义
的几何意义
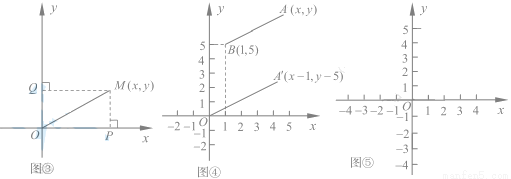
如图④,在直角坐标系中,设点 A'的坐标为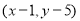 ,由探究(二)(1)可知,
,由探究(二)(1)可知,
A'O=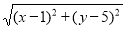 ,将线段 A'O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时A的坐标为(
,将线段 A'O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时A的坐标为(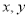 ),点B的坐标为(1,5)。
),点B的坐标为(1,5)。
因为AB= A'O,所以 AB=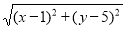 ,因此
,因此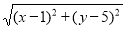 的几何意义可以理解为点A(
的几何意义可以理解为点A(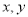 )与点B(1,5)之间的距离。
)与点B(1,5)之间的距离。
(3)探究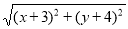 的几何意义
的几何意义
请仿照探究二(2)的方法,在图⑤中画出图形,并写出探究过程。
(4)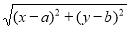 的几何意义可以理解为:_________________________.
的几何意义可以理解为:_________________________.
拓展应用:
(1)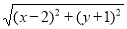 +
+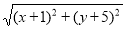 的几何意义可以理解为:点A
的几何意义可以理解为:点A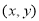 与点E
与点E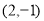 的距离与点AA
的距离与点AA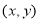 与点F____________(填写坐标)的距离之和。
与点F____________(填写坐标)的距离之和。
(2)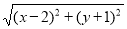 +
+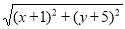 的最小值为____________(直接写出结果)
的最小值为____________(直接写出结果)
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(山东临沂卷)数学(解析版) 题型:解答题
数学课上,张老师出示了问题:如图1,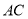 、
、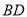 是四边形
是四边形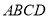 的对角线,若
的对角线,若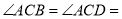
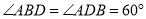 ,则线段
,则线段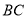 ,
,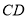 ,
,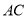 三者之间有何等量关系?
三者之间有何等量关系?
经过思考,小明展示了一种正确的思路:如图2,延长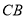 到
到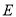 ,使
,使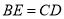 ,连接
,连接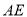 ,证得
,证得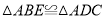 ,从而容易证明
,从而容易证明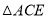 是等边三角形,故
是等边三角形,故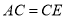 ,所以
,所以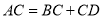 .
.
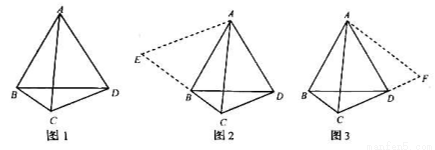
小亮展示了另一种正确的思路:如图3,将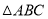 绕着点
绕着点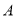 逆时针旋转
逆时针旋转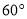 ,使
,使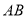 与
与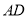 重合,从而容易证明
重合,从而容易证明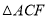 是等比三角形,故
是等比三角形,故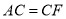 ,所以
,所以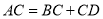 .
.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图4,如果把“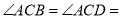
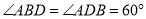 ”改为“
”改为“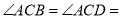
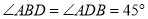 ”,其它条件不变,那么线段
”,其它条件不变,那么线段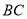 ,
,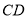 ,
,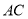 三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.
三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.
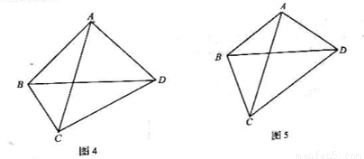
(2)小华提出:如图5,如果把“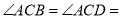
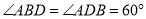 ”改为“
”改为“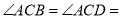
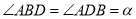 ”,其它条件不变,那么线段
”,其它条件不变,那么线段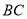 ,
,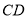 ,
,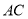 三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.
三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(山东东营卷)数学(解析版) 题型:选择题
如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=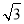 ,则△ABC移动的距离是( )
,则△ABC移动的距离是( )
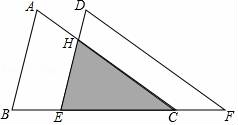
A.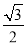 B.
B.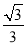 C.
C.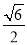 D.
D.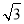 ﹣
﹣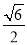
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com