练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知△ABC内接于⊙O，AO是半径，AD⊥BC于点Ｄ．求证：∠BAD＝∠OAC．

     

    答案：
    解析：

    		证法一：如图，延长AO交⊙O于E，连结CE．

    ∵AE是⊙O的直径，∴∠ACE＝90°．

    又AD⊥BC，∴∠ADB＝90°  ∵∠B＝∠E，∴∠BAD＝∠OAC．

    证法二：如图，作OE⊥AB交⊙O于E，交AB于F，连结OB．

    ∵OE⊥AB，∴＝．

    ∴∠AOE的度数＝的度数，∠C的度数＝的度数．

    ∴∠AOE＝∠C．

    ∵AD⊥BC，∴∠OFA＝∠ADC＝90°．

    ∴ ∠FAO＝∠DAC．

    ∴∠FAO＋∠OAD＝∠DAC＋∠OAD，∴∠BAD＝∠OAC．

     

    证法三：如图，连结OB，作OF⊥AB于F．

    ∵AO＝OB，∴OF平分∠AOB，∴∠AOF＝∠AOB，∵∠C＝∠AOB

    ∴∠C＝∠AOF，

    ∵AD⊥BC，∴∠AFO＝∠ADC＝90°．

    ∴∠FAO＝∠DAC．

    而∠FAO＋∠OAD＝∠DAC＋∠OAD，

    ∴∠FAD＝∠OAC．

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网如图，已知△ABC内接于⊙O，D是⊙O上一点，连接BD、CD、AC、BD交于点E．
    （1）请找出图中的相似三角形，并加以证明；
    （2）若∠D=45°，BC=2，求⊙O的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

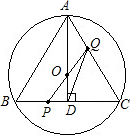    如图，已知△ABC内接于⊙O，AB=BC=4cm，AO⊥BC于D，点P、Q分别从B、C两点同时出发，其中点P沿BC向精英家教网终点C运动，速度为1cm/s；点Q沿CA向终点A运动，速度为2cm/s，设它们运动的时间为x（s）．
    （1）求证：△ABC为等边三角形；
    （2）当x为何值时，PQ⊥AC；
    （3）当PQ经过圆心O时，求△PQD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    15、已知△ABC内接于⊙O，AD，BD为⊙O的切线，作DE∥BC，交AC于E，连EO并延长交BC于F，求证：BF=FC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•樊城区模拟）如图，已知△ABC内接于⊙O，弦AD交BC于E，过点D的切线MN交直线AB于M，交直线AC于N．
    （1）求证：AE•DE=BE•CE；
    （2）连接DB，CD，若MN∥BC，试探究BD与CD的数量关系；
    （3）在（2）的条件下，已知AB=6，AN=15，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•永州）如图，已知△ABC内接于⊙O，BC是⊙O的直径，MN与⊙O相切，切点为A，若∠MAB=30°，则∠B=
    60
    60
    度．

    查看答案和解析>>

    同步练习册答案