解:(1)∵由x=0,得y=3.
∴点A的坐标为A(0,3).
∵二次函数y=-x
2+bx+c的图象经过点A(0,3)、B(1,0),
∴

,
解得

.
∴所求二次函数的解析式为y=-x
2-2x+3.顶点D的坐标为D(-1,4).
(2)设平移后的图象解析式为y=-(x+1)
2+k.
根据题意,可知点C(-1,k)在一次函数y=x+3的图象上,
则-1+3=k
解得k=2.
故所求图象的表达式为y=-(x+1)
2+2.
(3)设直线x=-1与x轴交于点E.
由(2)得 C(-1,2).
又由 A(0,3),得AC=
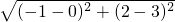
=

.
根据题意,设点P的坐标为P(m,m+3).
∵△ABP与△ABC同高,
于是,当S
△ABP=2S
△ABC时,得AP=2AC=2

.
此时,有两种不同的情况:
(ⅰ)当点P在线段CA的延长线上时,得CP=CA+AP=3

,且m>0.
过点P作PQ
1垂直于x轴,垂足为点Q
1.
易得
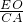
=
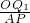
.

=
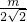
,
解得m=2.
m+3=5.
∴P
1(2,5).
(ⅱ)当点P在线段AC的延长线上时,得 CP=AP-CA=

,且m<0.
过点P作PQ
2垂直于x轴,垂足为点Q
2.
易得

=
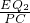
.

=
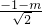
,
解得m=-2.
m+3=1.
∴P
2(-2,1).
综上所述,点P的坐标为(2,5)或(-2,1).
另解:(3)由(2)得 C(-1,2).
又由 A(0,3),得AC=
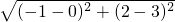
=

.
根据题意,设点P的坐标为P(m,m+3).
∵△ABP与△ABC同高,
于是,当S
△ABP=2S
△ABC时,得AP=2AC=2

∴AP
2=8.
即得m
2+(m+3-3)
2=8.
解得m
1=2,m
2=-2.
∴m+3=5或1.
∴点P的坐标为(2,5)或(-2,1).
分析:(1)先求出点A的坐标,再将点A(0,3)、B(1,0)代入二次函数y=-x
2+bx+c,可得方程组,解方程组求解即可得到二次函数的解析式;
(2)平移后的图象解析式为y=-(x+1)
2+k.根据点C(-1,k)在一次函数y=x+3的图象上,可得关于k 的方程,求得k的值,从而即可求出平移后所得图象的表达式;
(3)先根据两点间的距离公式得到AC的长,由S
△ABP=2S
△ABC,可得AP=2AC,再分(ⅰ)当点P在线段CA的延长线上时;(ⅱ)当点P在线段AC的延长线上时;两种情况讨论即可求解.
点评:考查了二次函数综合题,涉及的知识点有:待定系数法求函数的解析式,平移的性质,两点间的距离公式,分类思想的运用,综合性较强,有一定的难度.

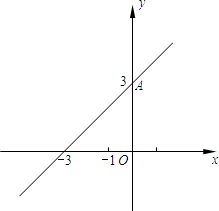 已知:在平面直角坐标系中,一次函数y=x+3的图象与y轴相交于点A,二次函数y=-x2+bx+c的图象经过点A、B(1,0),D为顶点.
已知:在平面直角坐标系中,一次函数y=x+3的图象与y轴相交于点A,二次函数y=-x2+bx+c的图象经过点A、B(1,0),D为顶点. ,
, .
.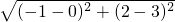 =
= .
. .
. ,且m>0.
,且m>0.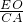 =
=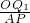 .
. =
=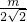 ,
, ,且m<0.
,且m<0. =
=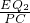 .
. =
=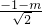 ,
,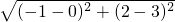 =
= .
.


 寒假学与练系列答案
寒假学与练系列答案
 如图,在平面直角坐标中,已知直线y=kx+b与直线y=
如图,在平面直角坐标中,已知直线y=kx+b与直线y= 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=