
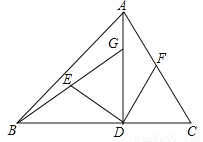
如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.
科目:初中数学 来源:2017-2018学年江苏省兴化市顾庄学区七年级上学期期末考试数学试卷 题型:填空题
单项式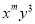 与单项式
与单项式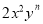 是同类项,则
是同类项,则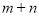 的值是________.
的值是________.
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2017-2018学年七年级(上)月考数学试卷 题型:单选题
如果收入200元记作+200元,那么支出150元记作( )
A. +150元 B. ﹣150元 C. +50元 D. ﹣50元
B 【解析】试题分析:具有相反意义的量是指:意义相反,与值无关.收入为正,则支出为负.查看答案和解析>>
科目:初中数学 来源:2017-2018学年云南省腾冲市七年级上学期期末考试数学试卷 题型:单选题
如图所示的几何体,从左面看到的平面图形是( ).
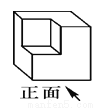
A. 
B. 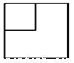
C. 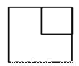
D. 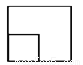
查看答案和解析>>
科目:初中数学 来源:2017-2018学年广东省八年级12月月考数学试卷 题型:解答题
对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|叫做P1、P2两点间的直角距离,记作d(P1,P2).
(1) 令P0(2,-3),O为坐标原点,则d(O,P0)= ;
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=1,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(3)设P0(x0,y0)是一定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做P0到直线y=ax+b的直角距离. 若P(a,-3)到直线y=x+1的直角距离为6,求a的值.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年广东省八年级12月月考数学试卷 题型:填空题
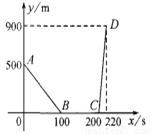
设甲、乙两车在同一直线公路上匀速行驶,开始时甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车上的货物转给甲车,然后甲车继续前行,乙车向原地返回、.设xs后两车间的距离为ym,y与x的函数关系如图所示,则乙车的速度是_______m/s.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年广东省八年级12月月考数学试卷 题型:填空题
据国家旅游局统计,2017年端午小长假全国各大景点共接待游客约为82600000人次,数据82600000用科学记数法表示为_____________
【解析】【解析】 82600000=.故答案为: .查看答案和解析>>
科目:初中数学 来源:浙江省义乌市四校2017-2018学年七年级上学期第三次作业检测数学试卷 题型:解答题
计算: (1)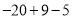 (2)
(2)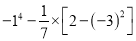
查看答案和解析>>
科目:初中数学 来源:初三数学第一学期1.2.1矩形的定义与性质 同步练习 题型:填空题
如图,矩形ABCD中,AD=3,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是_____.
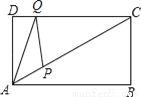
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com