Question

4．如图，以Rt△ABC的三边分别为直径向外作三个半圆，已知以AC为直径的半圆的面积为S₁，以BC为直径的半圆的面积为S₂，以AB为直径的半圆的面积为S．
（1）求证：S=S₁+S₂．
（2）若将图中半圆改为分别以三边为斜边的等腰直角三角形，如图2，探究（1）中的结论是否仍成立？

Answer 1

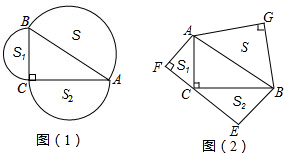
分析 （1）如图（1），设AC=λ，BC=μ，AB=γ；由勾股定理得：λ²+μ²=γ²；证明S₁+S₂=$\frac{π}{4}（{λ}^{2}+{μ}^{2}）$，$S=\frac{π{γ}^{2}}{4}$，即可解决问题．
（2）如图（2）设AC=λ，BC=μ，AB=γ；首先证明λ²+μ²=γ²；其次证明${S}_{1}+{S}_{2}=\frac{1}{4}（{λ}^{2}+{μ}^{2}）$，$S=\frac{1}{4}{γ}^{2}$，即可解决问题．

解答 解：（1）如图（1），设AC=λ，BC=μ，AB=γ；
∵△ABC为直角三角形，
∴λ²+μ²=γ²；
∵${S}_{1}+{S}_{2}=\frac{π{λ}^{2}}{4}+\frac{π{μ}^{2}}{4}=\frac{π}{4}（{λ}^{2}+{μ}^{2}）$，$S=\frac{π{γ}^{2}}{4}$，
∴S=S₁+S₂．
（2）如图（2），设AC=λ，BC=μ，AB=γ；
∵△ABC为直角三角形，
∴λ²+μ²=γ²；
∵△ABG为等腰直角三角形，
∴2AG²=AB²，即AG²=$\frac{1}{2}$γ²，
∴$S=\frac{1}{2}A{G}^{2}=\frac{1}{4}{γ}^{2}$；同理可求：
S₁+S₂=$\frac{1}{4}{λ}^{2}+\frac{1}{4}{μ}^{2}$=$\frac{1}{4}（{λ}^{2}+{μ}^{2}）$，
∴S=S₁+S₂．
即（1）中的结论仍然成立．

点评 该题主要考查了勾股定理及其应用问题；解题的关键是灵活运用勾股定理等几何知识点来分析、判断、推理或解答．