Question

如图（1），在平行四边形ABCD中，AE⊥BC于点E，E恰为BC的中点，tanB=2。
（1）求证：AD=AE；
（2）如图（2），点P在线段BE上，作EF⊥DP 于点F，连接AF，求证：DF-EF=AF；
（3）请你在图（3）中画图探究：当P为线段EC上任意一点（P不与点E重合）时，作EF垂直直线DP，垂足为点F，连接AE线段DF、EF与AF之间有怎样的数量关系？直接写出你的结论。

Answer 1

解：（1）在Rt△ABE中，∠AEB=90°， ∴tanB=AE/BE=2， ∴AE=2BE， ∵E为BC的中点， ∴ BC=2BE， ∴AE=BC， ∵四边形ABCD是平行四边形， ∴AD=BC， ∴AE=AD；
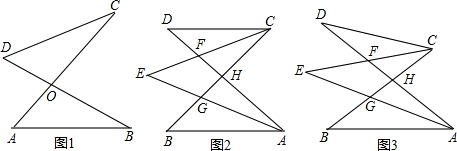
（2）证明：在DP上截取DH=EF（如图（1））， ∵四边形ABCD是平行四边形，AE⊥BC， ∴∠EAD=90°， ∵EF⊥PD，∠1=∠2， ∴∠ADH=∠AEF， ∵AD=AE， ∴△ADH≌△AEF， ∴∠HAD=∠FAE，AH=AF， ∴∠FAH=90°， 在Rt△FAH中，AH=AF， ∴ ∴FH=FD-HD=FD-EF， 即；
（3）按题目要求所画图形如图（2），线段DF、EF、AF之间的数量关系为： 。