练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，∠1＝，∠n2＝，∠3＝，求∠4．

    答案：
    解析：

    　　由于∠2＝，∠2＋∠5＝，

    　　所以∠5＝＝∠1．

    　　根据同位角相等，两直线平行．

    　　所以a∥b．再根据两直线平行，内错角相等．

    　　所以∠4＝∠3＝．

    　　剖析：由已知条件，不难发现∠1与∠2互补，而∠1与∠2的邻补角∠5是同位角，根据同角的补角相等以及同位角相等，两直线平行，可得a∥b．进而利用平行线的特征，即可求出∠4．


    提示：

    　　方法提炼：

    　　本题综合运用了平行线的识别和平行线的特征的有关知识，解答此类题目，一方面要善于“由角定线”，也就是根据角的相等或互补关系来判断出两直线平行；另一方面还要善于“由线定角”，即运用平行线的特征来确定两个角的关系．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：吉林省长春外国语学校2010-2011学年八年级上学期期中考试数学试题 题型：013

    如图是一个边长为m＋n的正方形，将图1中的阴影部分拼成图2中的形状，由图1和图2验证的式子是

    [　　]
    A．

    (m＋n)2－(m－n)2＝4mn

    B．

    (m＋n)2－(m2＋n2)＝2mn

    C．

    (m－n)2＋2mn＋m2＋n2

    D．

    (m＋n)(m－n)＝m2－n2

    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市相城区2011－2012学年八年级上学期期中测试数学试题 题型：047

    (1)在△ABC中，AB＝m2－n2，AC＝2mn，BC＝m2＋n2(m＞n＞0)．

    求证：△ABC是直角三角形；

    (2)已知：如图，在梯形ABCD中，AD∥BC，点E、F分别是AD、BC的中点，若AB＝m2－n2，CD＝2mn，AD＝n2，BC＝m2＋2n2，(m＞n＞0)．

    求证：EF＝(m2＋n2)．

    查看答案和解析>>

    科目：初中数学 来源：初中数学　三点一测丛书　八年级数学　下　（江苏版课标本） 江苏版 题型：044

    如图，已知△ABC中，DE∥BC，S△OBC＝n2，S△DOB＝mn(n＞m)，求S梯形BCED和S△ADE

    查看答案和解析>>

    科目：初中数学 来源：2015届湖北武汉部分学校八年级12月月考数学试卷（解析版） 题型：解答题

    如图（1），在平面直角坐标系中，AB⊥x轴于B，AC⊥y轴于C，点C（0，m），A（n，m），且（m-4）2+n2-8n＝-16，过C点作∠ECF分别交线段AB、OB于E、F两点.

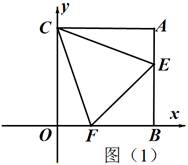
    （1）求A点的坐标（3分）；

    （2）若OF+BE＝AB，求证：CF＝CE（4分）

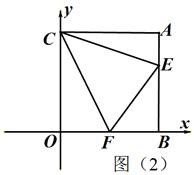
    （3）如图（2），若∠ECF＝45°，给出两个结论：OF+AE-EF的值不变；‚OF+AE+EF的值不变，其中有且只有一个结论正确，请你判断出正确的结论，并加以证明和求出其值（5分）.

     

     

    查看答案和解析>>

    同步练习册答案