
下列说法正确的是( )
A. 形状相同的两个三角形全等 B. 面积相等的两个三角形全等
C. 完全重合的两个三角形全等 D. 所有的等边三角形全等
C 【解析】试题分析:当两个三角形完全重合时,则两个三角形全等. 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:初中数学 来源:浙江省宁波市鄞州区2017-2018学年九年级上册数学第一次月考试卷 题型:解答题
某工厂准备翻建新的大门,厂门要求设计成轴对称的拱形曲线.已知厂门的最大宽度AB=12m,最大高度OC=4m,工厂的运输卡车的高度是3m,宽度是5.8m.现设计了两种方案.方案一:建成抛物线形状(如图1);方案二:建成圆弧形状(如图2).为确保工厂的卡车在通过厂门时更安全,你认为应采用哪种设计方案?请说明理由.
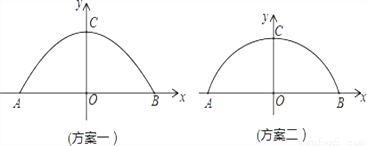
查看答案和解析>>
科目:初中数学 来源:江西婺源县2016-2017学年第一学期期末考试七年级数学试卷 题型:单选题
已知方程x2k-1 + k = 0是关于x的一元一次方程,则方程的解等于( )
A. -1 B. 1 C. 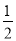 D. ﹣
D. ﹣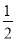
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市鄞州区九校2017-2018学年八年级上册数学第一次月考试卷 题型:填空题
等腰三角形的一个角是100°,则它顶角的度数是______
100° 【解析】当等腰三角形的一个角的度数为100°时,这个角一定是顶角,不可能是底角, 故答案为:100°.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市鄞州区九校2017-2018学年八年级上册数学第一次月考试卷 题型:单选题
如图所示,有以下三个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这三个条件中任选两个作为假设,另一个作为结论,则组成真命题的个数为( )
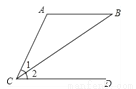
A. 0 B. 1 C. 2 D. 3
D 【解析】所有等可能的情况有3种,分别为①②⇒③;①③⇒②;②③⇒①,其中组成命题是真命题的情况有:①②⇒③;①③⇒②;②③⇒①, 故选:D.查看答案和解析>>
科目:初中数学 来源:2016-2017学年河北省张家口市桥东区七年级(下)期末数学试卷 题型:解答题
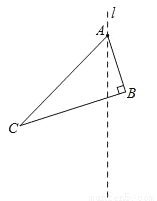
如图,已知Rt△ABC中,∠ABC=90°,经过点A的直线l与BC交于点F.
(1)请作出△ABC关于直线l轴对称的△ADE(A、B、C的对应点分别是A、D、E)
(2)连接CD,EB,在不添加其它辅助线的情况下,请你找出图中的一对全等三角形: ≌ ;
(3)证明(2)中的结论.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年河北省张家口市桥东区七年级(下)期末数学试卷 题型:单选题
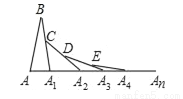
如图,在△ABA1中,∠B=20°,AB=A1B,在A1B 上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…,按此做法进行下去,∠An的度数为( )
A. 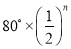 B.
B. 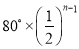 C.
C. 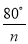 D.
D. 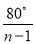
查看答案和解析>>
科目:初中数学 来源:辽宁省2017-2018学年八年级(上)期中数学试卷 题型:解答题
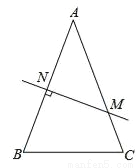
如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.
(1)若∠B=70°,则∠NMA的度数是 .
(2)连接MB,若AB=8cm,△MBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:湖北省黄冈市2017-2018学年八年级(上)期中数学试 题型:单选题
如图,E是等边三角形ABC中AC边上的点,∠1=∠2,BE=CD,则△ADE的形状是( )
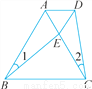
A. 一般等腰三角形 B. 等边三角形 C. 不等边三角形 D. 不能确定形状
B 【解析】试题分析:E是等边△ABC中AC边上的点,AB=AC;又因为∠1=∠2,BE=CD,所以,则AE=AD, ,所以△ADE的形状是等边三角形(有一个角是60度的等腰三角形是等边三角形)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com