


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
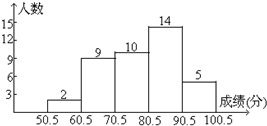 高分成五组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的信息,回答下列问题:
高分成五组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的信息,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
| x-3 |
| 4 |
| 3-4x |
| 2 |
|
| 1 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
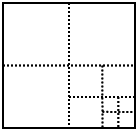 将一个边长为1的正方形纸片,剪成四个大小一样的正方形,然后将其中一个小正方形再按照同样的方法剪成四个正方形,如此循环下去,观察下列图表,回答下列问题:
将一个边长为1的正方形纸片,剪成四个大小一样的正方形,然后将其中一个小正方形再按照同样的方法剪成四个正方形,如此循环下去,观察下列图表,回答下列问题:| 操作次数 | 1 | 2 | 3 | 4 | … |
| 所得正方形的总个数 | 4 | 7 | 10 | 13 | … |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 128 |
| 1 |
| 256 |
查看答案和解析>>
科目:初中数学 来源: 题型:
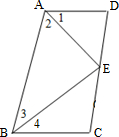 22、如图,四边形ABCD中,点E在边CD上,连接AE、BE,给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB,将其中的三个关系式作为题设,另外两个作为结论,便构成一个命题.
22、如图,四边形ABCD中,点E在边CD上,连接AE、BE,给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB,将其中的三个关系式作为题设,另外两个作为结论,便构成一个命题.查看答案和解析>>
科目:初中数学 来源: 题型:
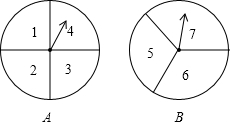 小亮获胜.
小亮获胜.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com