
如图,已知Rt△ABC中,∠C=90°,AC=4,tanA= ,则BC的长是( )
,则BC的长是( )
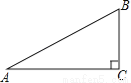
A. 2 B. 8 C. 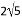 D.
D. 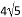
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:填空题
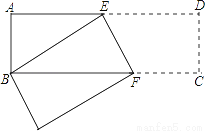
如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF.求△ABE的面积.
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:单选题
关于函数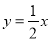 ,下列结论正确的是( )
,下列结论正确的是( )
A. 函数图象必经过点(1,2) B. 函数图象经过第二、四象限
C. y随x的增大而增大 D. 不论x取何值,总有y>0
C 【解析】根据正比例函数的性质,A、把(1,2)代入得:左边≠右边,故本选项错误;B、k=>0,图象经过一三象限,故本选项错误;C、k=>>0,y随x的增大而增大,故本选项正确;D、当x<0时y<0,故本选项错误. 故选:C.查看答案和解析>>
科目:初中数学 来源:湖南省邵阳县黄亭市2017~2018学年九年级数学(上)期末综合检测模拟题 题型:填空题
若关于x的一元二次方程x2 – 2x+k=0无实数根,则实数k的取值范围是____.
k>1 【解析】试题解析:∵关于x的一元二次方程x2-2x+k=0无实数根, ∴△=b2-4ac=(-2)2-4×1×k<0, ∴k>1.查看答案和解析>>
科目:初中数学 来源:湖南省邵阳县黄亭市2017~2018学年九年级数学(上)期末综合检测模拟题 题型:单选题
(2016山东省烟台市)反比例函数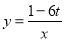 的图象与直线y=﹣x+2有两个交点,且两交点横坐标的积为负数,则t的取值范围是( )
的图象与直线y=﹣x+2有两个交点,且两交点横坐标的积为负数,则t的取值范围是( )
A. t<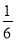 B. t>
B. t>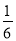 C. t≤
C. t≤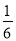 D. t≥
D. t≥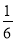
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省兰州市中考数学模拟试卷 题型:解答题
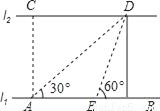
如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省兰州市中考数学模拟试卷 题型:填空题
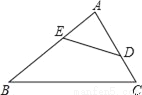
如图,在△ABC中,点D、E分别为边AC、AB上的点,且∠ADE=∠B,AE=3,BE=4,则AD•AC= .
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省兰州市中考数学模拟试卷 题型:单选题
如图所示的几何体是由5个大小相同的小正方体紧密摆放而成的,其三视图中面积最大的是( )
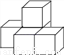
A. 主视图 B. 左视图 C. 俯视图 D. 主视图和俯视图
D 【解析】如图,该几何体主视图是由4个小正方形组成, 左视图是由3个小正方形组成, 俯视图是由4个小正方形组成,故三种视图面积最小的是左视图. 故选B.查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:单选题
如图,四个图形是由立体图形展开得到的,相应的立体图形顺次是( )

A. 正方体、圆柱、三 棱柱、圆锥
B. 正方体、圆锥、三棱柱、圆柱
C. 正方体、圆柱、三棱锥、圆锥
D. 正方体、圆柱 、四棱柱、圆锥
A 【解析】试题分析:根据正方体、圆柱、三棱柱、圆锥表面展开图的特点解题. 【解析】 观察图形,由立体图形及其表面展开图的特点可知相应的立体图形顺次是正方体、圆柱、三棱柱、圆锥. 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com