(1)证明:由题意,知△ABC≌△A
1B
1C
1,
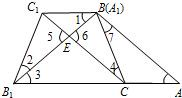
∴AB=A
1B
1,BC=B
1C
1,∠2=∠7,∠A=∠1.
∴∠3=∠A=∠1.
∴BC
1∥AC.
∴四边形ABC
1C是平行四边形.
∴AB∥CC
1.
∴∠4=∠7=∠2.
∵∠5=∠6,
∴∠B
1C
1C=∠B
1BC.
﹙2)解:∠A
1C
1C=∠A
1BC.
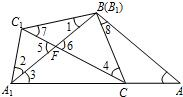
理由如下:由题意,知△ABC≌△A
1B
1C
1,
∴AB=A
1B
1,BC
1=BC,∠1=∠8,∠A=∠2.
∴∠3=∠A,∠4=∠7.
∵∠1+∠FBC=∠8+∠FBC,
∴∠C
1BC=∠A
1BA.
∵∠4=

(180°-∠C
1BC),∠A=

(180°-∠A
1BA),
∴∠4=∠A.
∴∠4=∠2
∵∠5=∠6,
∴∠A
1C
1C=∠A
1BC.
﹙3)解:△C
1FB,
△A
1C
1B,△ACB.﹙写对一个不得分﹚
分析:(1)由题意,知△ABC≌△A
1B
1C
1,根据矩形的性质及全等三角形的性质,可证四边形ABC
1C是平行四边形,再根据平行四边形的性质及相互间的等量关系即可得出;
(2)由题意,知△ABC≌△A
1B
1C
1,根据矩形的性质及全等三角形的性质,及相互间的等量关系即可得出;
(3)根据相似三角形的判定即可得出.
点评:本题主要考查了矩形的性质和全等三角形的性质,相似三角形的判定和性质等知识点,难度较大.





 (180°-∠C1BC),∠A=
(180°-∠C1BC),∠A= (180°-∠A1BA),
(180°-∠A1BA),

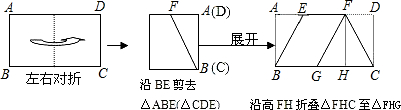
 如图,若将一张矩形风景画固定在相框架上,画四周留有相等宽度,则外框矩形ABCD与内框矩形EFGH
如图,若将一张矩形风景画固定在相框架上,画四周留有相等宽度,则外框矩形ABCD与内框矩形EFGH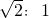 )时,它们相似
)时,它们相似