
分析 首先化简已知得出a=2,再将分式首先进行通分运算进而化简,把a的值代入即可.
解答 解:a=($\sqrt{3}$+2)(2-$\sqrt{3}$)2+$\sqrt{3}$
=(2+$\sqrt{3}$)(2-$\sqrt{3}$)(2-$\sqrt{3}$)+$\sqrt{3}$
=1×(2-$\sqrt{3}$)+$\sqrt{3}$
=2,
原式=$(\frac{a+1}{(a-1)(a+1)}-\frac{a-1}{(a-1)(a+1)})÷\frac{a}{2(a-1)(a+1)}$
=$\frac{2}{(a-1)(a+1)}×\frac{(a-1)(a+1)}{a}$
=$\frac{2}{a}$
当a=2时,原式=1.
点评 此题主要考查了二次根式的加减运算以及分式化简求值,正确化简分式是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | x1=-3,x2=-1 | B. | x1=1,x2=3 | C. | x1=-1,x2=3 | D. | x1=-3,x2=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
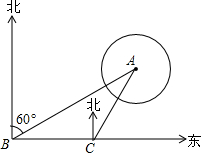 如图,某公园有一小亭A,它周围100米内是文物保持区,某勘探队员在公园由西向东行走,在B处测得小亭A在北偏东60°的方向上,行走200米后到达C处,此时测得小亭A在北偏东30°的方向上,若该公园打算沿BC的方向修一条笔直的小路,则此小路是否会通过文物保护区?请通过计算说明.
如图,某公园有一小亭A,它周围100米内是文物保持区,某勘探队员在公园由西向东行走,在B处测得小亭A在北偏东60°的方向上,行走200米后到达C处,此时测得小亭A在北偏东30°的方向上,若该公园打算沿BC的方向修一条笔直的小路,则此小路是否会通过文物保护区?请通过计算说明.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知⊙O1、⊙O2相交于A、B两点,直线O1O2交两圆于C、D两点.若∠O1AO2=40°,则∠CBD等于( )
如图,已知⊙O1、⊙O2相交于A、B两点,直线O1O2交两圆于C、D两点.若∠O1AO2=40°,则∠CBD等于( )| A. | 110° | B. | 120° | C. | 130° | D. | 140° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
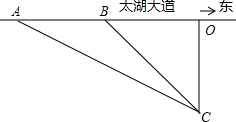 某同学为了检测车速,设计如下方案如图,观测点C选在东西方向的太湖大道上O点正南方向120米处.这时,一辆小轿车沿太湖大道由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为3秒,且∠ACO=60°,∠BCO=45°
某同学为了检测车速,设计如下方案如图,观测点C选在东西方向的太湖大道上O点正南方向120米处.这时,一辆小轿车沿太湖大道由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为3秒,且∠ACO=60°,∠BCO=45°查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{x}$+$\frac{x+2}{x+5}$=1 | B. | $\frac{2}{x}$+$\frac{x}{x+5}$=1 | C. | $\frac{2}{x}$+$\frac{x}{x-5}$=1 | D. | $\frac{2}{x}$+$\frac{x+2}{x-5}$=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com