练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    甲、乙两人进行射击练习，两人在相同条件下各射靶5次，射击成绩统计如下：

    命中环数（单位：环）

    7

    8

    9

    10

    甲命中相应环数的次数

    2

    2

    0

    1

    乙命中相应环数的次数

    1

    3

    1

    0

    则甲、乙两人射击成绩的平均数分别是 （单位：环）（　　）

    A. 5、5 B. 40、40 C. 8、8 D. 25、24

    C 【解析】由题意得： 甲=； 乙=. ∴甲、乙两人射击成绩的平均数分别是8和8. 故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省扬州市邗江区2018届九年级（上）期中数学试卷 题型：解答题

    如图，⊙O是△ABC的外接圆，∠ABC=45°，AD是⊙O的切线交BC的延长线于D，AB交OC于E．

    （1）求证：AD∥OC；

    （2）若AE=2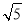，CE=2．求⊙O的半径和线段BE的长．

    （1）证明见解析；（2）． 【解析】 试题分析：（1）连结OA，根据切线的性质得到OA⊥AD，再根据圆周角定理得到∠AOC=2∠ABC=90°，然后根据平行线的判定即可得到结论； （2）设⊙O的半径为R，则OA=R，OE=R-2，AE=2，在Rt△OAE中根据勾股定理可计算出R=4；作OH⊥AB于H，根据垂径定理得AH=BH，再利用面积法计算出OH=，然后根据勾股定理计算出AH=...

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省扬州市中考数学模拟试卷（二） 题型：填空题

    函数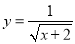中，自变量x的取值范围是 ；

    【解析】当函数表达式是分式时，考虑分式的分母不能为0；当分母上是二次根式时还要考虑被开方数为非负数, ：∵在分母上， ∴x+2＞0．，即

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省中考数学模拟试卷 题型：解答题

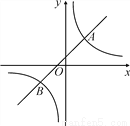
    (8分)如图，在平面直角坐标系xOy中，一次函数y＝kx＋b的图象与反比例函数y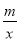＝的图象交于A(2，3)，B(－3，n)两点．

    (1)求一次函数和反比例函数的解析式；

    (2)若P是y轴上一点，且满足△PAB的面积是5，求OP的长．

    （1）y=x+1；（2）1 【解析】试题分析：（1）将A坐标代入反比例函数解析式中求出m的值，即可确定出反比例函数解析式；设直线AB解析式为y=kx+b，将B坐标代入反比例解析式中求出n的值，确定出B坐标，将A与B坐标代入一次函数解析式中求出k与b的值，即可确定出一次函数解析式； （2）如图所示，对于一次函数解析式，令x=0求出y的值，确定出C坐标，得到OC的长，三角形ABP面积由三角...

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省中考数学模拟试卷 题型：填空题

    在3□2□（﹣2）的两个空格□中，任意填上“+”或“﹣”，则运算结果为3的概率是 ．

    【解析】 试题分析：∵共有4种情况，而结果为3的有：3+2+（﹣2）=3，3﹣2﹣（﹣2）=3， ∴P（3）=． 故本题答案为：．

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省中考数学模拟试卷 题型：单选题

    下列关于分式的判断，正确的是( )

    A. 当x=2时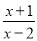， 的值为零

    B. 无论x为何值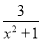， 的值总为正数

    C. 无论x为何值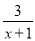， 不可能得整数值

    D. 当x≠3时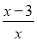， 有意义

    B 【解析】A选项中，因为当时，分式无意义，所以本选项错误； B选项中，因为无论取何值， 的值始终为正数，则分式的值总为正数，所以本选项正确； C选项中，因为当时，分式，所以本选项说法错误； D选项中，因为时，分式才有意义，所以本选项说法错误； 故选B.

    查看答案和解析>>

    科目：初中数学 来源：江西省2017年秋人教七年级数学上册期末模拟卷 题型：单选题

    如图，∠ACB=900，AC=BC，BE⊥CE，AD⊥CE于D，AD=2.5cm，DE=1.7cm，则BE=（ ）

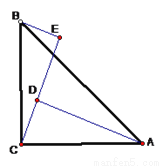
    A. 1cm B. 0.8cm C. 4.2cm D. 1.5cm

    B 【解析】试题解析： ∵BE⊥CE，AD⊥CE， ∴∠BCE=∠CAD， 在△ACD和△CBE中， ∴△ACD≌△CBE(AAS)， ∴AD=CE=2.5cm，BE=CD， ∵CD=CE?DE=2.5?1.7=0.8cm， ∴BE=0.8cm. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：河北省2017-2018学年九年级第一学期第一次月考数学试卷 题型：单选题

    已知一组数据a，b，c的平均数为5，方差为4，那么数据a﹣2，b﹣2，c﹣2的平均数和方差分别是.（　　）

    A. 3，2 B. 3，4 C. 5，2 D. 5，4

    B 【解析】试题分析：平均数为（a?2 + b?2 + c?2 ）=（3×5-6）=3；原来的方差：；新的方差：，故选B.

    查看答案和解析>>

    科目：初中数学 来源：山东省聊城市莘县2017-2018学年八年级（上）期末模拟数学试卷（含答案） 题型：解答题

    如图，△ABC是边长为5cm的等边三角形，点P，Q分别从顶点A，B同时出发，沿射线AB，BC运动，且它们的速度都为2cm/s．设点P的运动时间为t（s）．

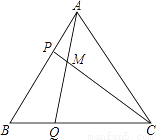
    （1）当t为何值时，△ABQ≌△CBP．

    （2）连接AQ、CP，相交于点M，则点P，Q在运动的过程中，∠CMQ会变化吗？若变化，则说明理由；若不变，请求出它的度数．

    （1）t=s时，△ABQ≌△CBP； （2）结论∠CMQ=60°不变，理由见解析. 【解析】试题分析:(1)根据△ABQ≌△CBP,利用全等三角形的性质可得:BQ=BP,根据动点运动的速度用含t的代数式表示出BQ和BP,列方程即可求解, (2)根据三角形外角性质可得:∠CMQ=∠CAM+∠ACM,根据△ABQ≌△CBP可得∠BAQ=∠ACM,等量代换可得∠CMQ=∠CAM+∠BA...

    查看答案和解析>>

    同步练习册答案