
解不等式组: 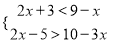 .
.
科目:初中数学 来源:2017年安徽省六安市中考数学模拟试卷(4月份) 题型:解答题
已知二次函数y=x2+bx+c的图象经过点(0,2)和(1,﹣1),求图象的顶点坐标和对称轴.
顶点坐标是(2,﹣2),对称轴是直线x=2. 【解析】试题分析: 要求二次函数的顶点坐标和对称轴,需要得到二次函数的解析式. 因为条件中的两点均在该二次函数的图象上,所以这两点的横纵坐标应该满足该二次函数的解析式. 将相应坐标代入解析式就得到了一个关于待定系数b与c的二元一次方程组,进而容易求得该二次函数的解析式. 由于该解析式符合二次函数的一般形式,可以通过相关公式求得顶点坐标和对称...查看答案和解析>>
科目:初中数学 来源:2017年湖北省随州市中考数学模拟试卷 题型:解答题
已知二次函数y=x2﹣2mx+4m﹣8,
(1)当x≤2时,函数值y随x的增大而减小,求m的取值范围.
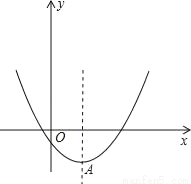
(2)以抛物线y=x2﹣2mx+4m﹣8的顶点A为一个顶点作该抛物线的内接正三角形AMN(M,N两点在拋物线上),请问:△AMN的面积是与m无关的定值吗?若是,请求出这个定值;若不是,请说明理由.
(3)若抛物线y=x2﹣2mx+4m﹣8与x轴交点的横坐标均为整数,求整数m的最小值.
查看答案和解析>>
科目:初中数学 来源:2017年湖北省随州市中考数学模拟试卷 题型:单选题
在娱乐节目“墙来了!”中,参赛选手背靠水池,迎面冲来一堵泡沫墙,墙上有人物造型的空洞.选手需要按墙上的造型摆出相同的姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一块几何体恰好能以右图中两个不同形状的“姿势” 分别穿过这两个空洞,则该几何体为( )
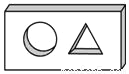
A. 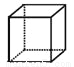 B.
B. 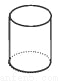 C.
C. 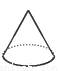 D.
D. 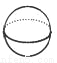
查看答案和解析>>
科目:初中数学 来源:2017年天津九中中考数学冲刺试卷 题型:解答题
如图,抛物线y=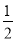 x2﹣
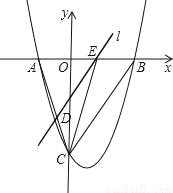
x2﹣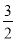 x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源:2017年天津九中中考数学冲刺试卷 题型:填空题
分解因式2x2﹣4x+2的最终结果是_____.
2(x﹣1)2 【解析】试题分析:先提取公因式2,再根据完全平方公式进行二次分解. 试题解析:2x2-4x+2, =2(x2-2x+1), =2(x-1)2.查看答案和解析>>
科目:初中数学 来源:2017年天津九中中考数学冲刺试卷 题型:单选题
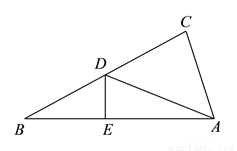
某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
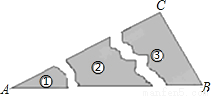
A. 带①去 B. 带②去 C. 带③去 D. ①②③都带去
C 【解析】试题解析:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的; 第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带③去. 故选C.查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2017-2018学年度上学期期中考试七年级数学试卷 题型:解答题
某出租车司机国庆节的营运全是在长虹路南北方向上进行的,如果规定向北为正,向南为负,他这天行车里程(单位:千米)如下: 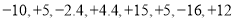
(1) 最后一名乘客送到目的地时,出租车在出发点的哪个方向?与出发点的距离?
(2) 长虹路南北至少有多少千米?
(3) 若该出租车耗油量为每千米0.08升,每升油7.5元,出租车按物价部门规定,起步价(不超过3千米)5元,超过3千米的部分,每千米(不足1千米按1千米计算)加价2元,该出租车司机今天的纯收入为多少元?(纯收入=收入-油耗钱)
(1) 13千米处;(2) 27千米; (3) 92.12元. 【解析】试题分析:(1)把记录下来的数字相加即可得到结果; (2)求出八次运营与出发点的距离,即可得出结论; (3)把记录下来的数字求出绝对值之和,乘以0.08和7.5即可得到结果. 试题解析:【解析】 (1)∵-10+5-2.4+4.4+15+5-16+12=+13. ∴最后一名乘客下车时,出租车在出...查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初二上期中试卷数学试卷 题型:单选题
如图,将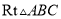 纸片的直角边
纸片的直角边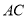 沿直线
沿直线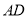 折叠,使它落在斜边
折叠,使它落在斜边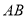 上,且与
上,且与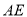 重合,若
重合,若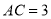 ,
, 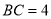 ,则
,则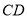 的长为( ).
的长为( ).
A. 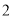 B.
B. 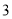 C.
C. 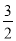 D.
D. 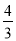
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com