
 如图,双曲线y=
如图,双曲线y= 上两点A、B,xB=2xA=2,AF∥x轴,AC∥OF交OB于E,且S四边形ABOF=
上两点A、B,xB=2xA=2,AF∥x轴,AC∥OF交OB于E,且S四边形ABOF= ,则k=________.
,则k=________. ,由S五边形AFOMB=S四边形ABOF+S△OBM=
,由S五边形AFOMB=S四边形ABOF+S△OBM= +
+ ,进而得出S五边形AFOMB=S四边形AFOC+S四边形ACMB=
,进而得出S五边形AFOMB=S四边形AFOC+S四边形ACMB= k,进而求出即可.
k,进而求出即可.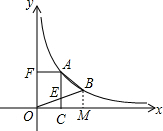 解:过点B作BM⊥x轴于点M,
解:过点B作BM⊥x轴于点M, 上两点A、B,xB=2xA=2,
上两点A、B,xB=2xA=2, ,
, ,
, ,
, ×BM×MO=
×BM×MO= ,
, +
+ ,
, (AC+BM)×MC=k+
(AC+BM)×MC=k+ k=
k= k=
k= +
+ ,
,

科目:初中数学 来源: 题型:
| 1 |
| 2 |
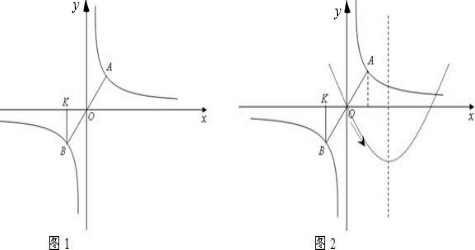
 x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+
x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+| 9 |
| 2 |
| m |
| x |
| m |
| x |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 12 |
| x |
| 1 |
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图.反比例函数y=-
如图.反比例函数y=-| 8 |
| x |
| 8 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
| 1 |
| x |
| 3 |
| x |

查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市初九年级上学期第二次阶段测数学试卷(解析版) 题型:填空题
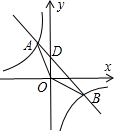
如图,双曲线 经过
经过 的两个顶点
的两个顶点 、
、 轴,连接
轴,连接 ,将
,将 沿
沿 翻折后得到
翻折后得到 ,点
,点 刚好落在线段
刚好落在线段 上,连接
上,连接 ,
, 恰好平分
恰好平分 与
与 轴负半轴的夹角,若
轴负半轴的夹角,若 的面积为3,则
的面积为3,则 的值为
。
的值为
。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com