
 + bx +c����A��C���㣬��x�����һ����ΪG��M��FG���е㣬������CDEF�����Ϊ1��
+ bx +c����A��C���㣬��x�����һ����ΪG��M��FG���е㣬������CDEF�����Ϊ1��
 (��ȥ).
(��ȥ). 


 ����PFE=�� FEM= 90��.
����PFE=�� FEM= 90��. 



 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012�콭��ʡ�����г���Ƭ���꼶��ѧ�����м����ѧ�Ծ����������� ���ͣ������
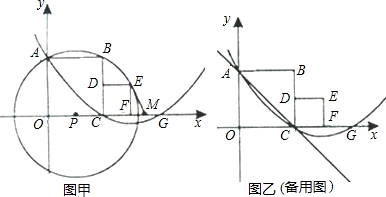
��ͼ�ף��ֱ��������˴����ڵ�������OABC��CDEF�ı�OC��OA����ֱ��Ϊ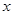 �ᡢ
�ᡢ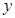 �Ὠ��ƽ��ֱ������ϵ��O��C��F������x���������ϣ�.����P��A��B��E����(Բ����
�Ὠ��ƽ��ֱ������ϵ��O��C��F������x���������ϣ�.����P��A��B��E����(Բ����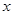 ����)��������
����)��������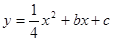 ����A��C���㣬��
����A��C���㣬��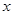 �����һ����ΪG��M��FG���е㣬������CDEF�����Ϊ1.
�����һ����ΪG��M��FG���е㣬������CDEF�����Ϊ1.
��С��1����B�����ꣻ
��С��2����֤��ME�ǡ�P�����ߣ�
��С��3����ֱ��AC�������߶Գ��ύ��N��Q���Ǵ˶Գ����ϲ���N���غϵ�һ���㣬�����ACQ�ܳ�����Сֵ������FQ��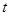 ����ACQ����� S��ACQ��
����ACQ����� S��ACQ��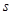 ��ֱ��д��
��ֱ��д��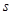 ��
��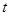 ֮��ĺ�����ϵʽ.
֮��ĺ�����ϵʽ.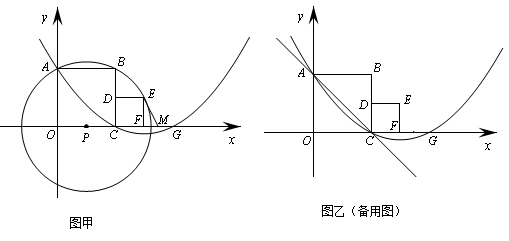
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012ѧ�꽭��ʡ�����н����гζ�Ƭ���꼶���£�������ѧ�Ծ��������棩 ���ͣ������
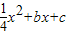 ����A��C���㣬��x�����һ����ΪG��M��FG���е㣬������CDEF�����Ϊ1��
����A��C���㣬��x�����һ����ΪG��M��FG���е㣬������CDEF�����Ϊ1��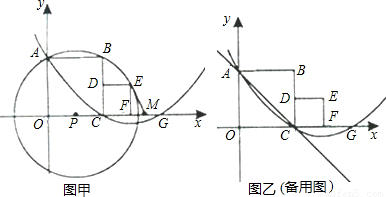
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012�꽭��ʡ�����н������п���ѧģ���Ծ���4�·ݣ��������棩 ���ͣ������
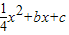 ����A��C���㣬��x�����һ����ΪG��M��FG���е㣬������CDEF�����Ϊ1��
����A��C���㣬��x�����һ����ΪG��M��FG���е㣬������CDEF�����Ϊ1��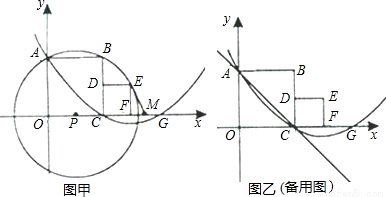
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011�����ʡ�������п���ѧ�Ծ��������棩 ���ͣ������
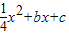 ����A��C���㣬��x�����һ����ΪG��M��FG���е㣬������CDEF�����Ϊ1��
����A��C���㣬��x�����һ����ΪG��M��FG���е㣬������CDEF�����Ϊ1��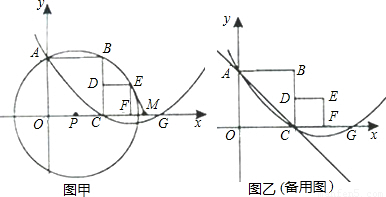
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com