
 如图,半径为3的⊙O与Rt△AOB的斜边AB切于点D,交OB于点C,连接CD交直线OA于点E,若∠B=30°,则线段AE的长为$\sqrt{3}$.
如图,半径为3的⊙O与Rt△AOB的斜边AB切于点D,交OB于点C,连接CD交直线OA于点E,若∠B=30°,则线段AE的长为$\sqrt{3}$. 分析 要求AE的长,只要求出OA和OE的长即可,要求OA的长可以根据∠B=30°和OB的长求得,OE可以根据∠OCE和OC的长求得.
解答 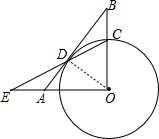 解:连接OD,如右图所示,
解:连接OD,如右图所示,
由已知可得,∠BOA=90°,OD=OC=3,∠B=30°,∠ODB=90°,
∴BO=2OD=6,∠BOD=60°,
∴∠ODC=∠OCD=60°,AO=BO•tan30°=$6×\frac{\sqrt{3}}{3}=2\sqrt{3}$,
∵∠COE=90°,OC=3,
∴OE=OC•tan60°=$3×\sqrt{3}=3\sqrt{3}$,
∴AE=OE-OA=$3\sqrt{3}-2\sqrt{3}=\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查切线的性质,解题的关键是明确题意,找出所求问题需要的条件.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{{\begin{array}{l}{8x-3=y}\\{7x+4=y}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{8x+3=y}\\{7x-4=y}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{y-8x=3}\\{y-7x=4}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{8x-y=3}\\{7x-y=4}\end{array}}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:| A. | ②④⑤⑥ | B. | ①③⑤⑥ | C. | ②③④⑥ | D. | ①③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
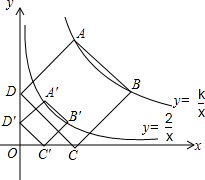 如图,正方形ABCD的顶点A,B在函数y=$\frac{k}{x}$(x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.
如图,正方形ABCD的顶点A,B在函数y=$\frac{k}{x}$(x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
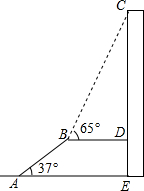 如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
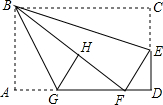 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com