练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如果＝＝，求证：x＋y＝－z．

    答案：
    解析：

    　　证明：设＝＝＝k，

    　　则x＝k(a－b)，y＝k(b－c)，z＝k(c－a)．

    　　∴x＋y＝k(a－b)＋k(b－c)

    　　＝k(a－c)＝－k(c－a)，

    　　∴x＋y＝－z．


    提示：

    　　点悟：给出的条件，若想分离出x，y，z，只有应用其连比相等这一条件，设其等于k，引入参数k，即可为证明等式创造条件．

    　　点拨：此题的关键在于引进了参数k，化分式为整式，这种将连比形式用k表达，统一其条件的方法，是解连比式为条件的题目的常用方法．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2011年浙江省义乌市初中毕业生学业考试模拟数学卷 题型：解答题

    (本题6分) 已知：如图，在△ABC中， D是BC边上的一点，E是AD的中点，过点A作BC的平行线交与BE的延长线于点F，且AF＝DC,连结CF．

    【小题1】（1）求证：D是BC的中点；
    【小题2】（2）如果AB＝AC，试判断四边形ADCF的形状，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源：2011～2012贵州普安县江西坡镇民族中学九年级上期末测试数学试卷（带解析） 题型：解答题

    如图：AB是⊙O的直径，以OA为直径的⊙O1与⊙O的弦AC相交于D，DE⊥OC，垂足为E。

    （1）求证：AD＝DC
    （2）求证：DE是的切线
    （3）如果OE＝EC，请判断四边形O1OED是什么四边形，并证明你的结论。

    查看答案和解析>>

    科目：初中数学 来源：2013-2014学年四川富顺骑龙学区九年级上学期期中检测数学试卷（解析版） 题型：解答题

    如图：AB是⊙O的直径，以OA为直径的⊙O1与⊙O的弦AC相交于D，DE⊥OC，垂足为E．

    （1）求证：AD＝DC

    （2）求证：DE是⊙O1的切线

    （3）如果OE＝EC，请判断四边形O1OED是什么四边形，并证明你的结论．

     

    查看答案和解析>>

    科目：初中数学 来源：2011-2012贵州普安县江西坡镇民族中学九年级上期末测试数学试卷（解析版） 题型：解答题

    如图：AB是⊙O的直径，以OA为直径的⊙O1与⊙O的弦AC相交于D，DE⊥OC，垂足为E。

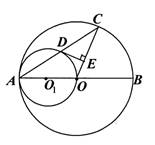
    （1）求证：AD＝DC

    （2）求证：DE是的切线

      （3）如果OE＝EC，请判断四边形O1OED是什么四边形，并证明你的结论。

     

    查看答案和解析>>

    同步练习册答案