
不等式组 的整数解是______.
的整数解是______.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:四川省遂宁市2018届九年级上学期教学水平监测数学试卷 题型:单选题
下列图形中不是位似图形的是
A. 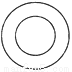 B.
B. 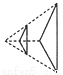 C.
C. 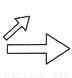 D.
D. 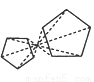
查看答案和解析>>
科目:初中数学 来源:2018春季学北师大版九年级数学下册期中测评试卷 题型:解答题
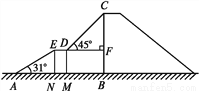
下图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4 m,AB=6 m,中间平台宽度DE=1 m,EN,DM,CB为三根垂直于AB的支柱,垂足分别为N,M,B,∠EAB=31°,DF⊥BC于点F,∠CDF=45°,求DM和BC的水平距离BM的长度.(结果精确到0.1 m.参考数据:sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)
查看答案和解析>>
科目:初中数学 来源:2018春季学北师大版九年级数学下册期中测评试卷 题型:单选题
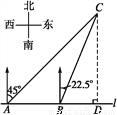
如图,在笔直的海岸线l上有A,B两个观测站,AB=2 km,从A处测得船C在北偏东45°的方向,从B处测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
A. 4 km B. 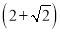 km C. 2
km C. 2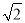 km D.
km D. 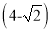 km
km
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(人教版)期末检测题 题型:解答题
已知小明骑车和步行的速度分别为240米/分,80米/分,小红每次从家步行到学校所需时间相同.请你根据小红和小明的对话内容(如图),求小明从家到学校的路程和小红从家步行到学校所需的时间.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(人教版)期末检测题 题型:填空题
已知5x-2的立方根是-3,则x+69的算术平方根是___________;
8 【解析】∵5x-2的立方根是-3,∴5x-2=-27, ∴x=-5; ∴x+69=-5+69=64, ∴x+69的算术平方根是 .查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(人教版)期末检测题 题型:单选题
如图,在铁路旁有一李庄O,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
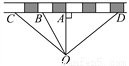
A. A点 B. B点 C. C点 D. D点
A 【解析】试题解析:根据垂线段最短可得:应建在A处, 故选A.查看答案和解析>>
科目:初中数学 来源:湖北省武汉市洪山区2018届九年级(上)期中数学试卷 题型:填空题
已知点P的坐标是(2,﹣3),那么点P关于原点的对称点P1的坐标是_____.
(2,﹣3) 【解析】试题解析:∵点P的坐标是(2,﹣3), ∴点P关于原点的对称点P1的坐标是(﹣2,3). 故答案为:(﹣2,3),查看答案和解析>>
科目:初中数学 来源:四川省西昌市2017-2018学年九年级数学(上)期末模拟试卷 题型:填空题
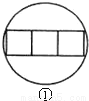
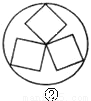
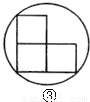
在一节数学实践活动课上,老师拿出三个边长都为5cm的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大?问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如下图所示:
(1)计算(结果保留根号与π).
(Ⅰ)图①能盖住三个正方形所需的圆形硬纸板最小直径应为 cm;
(Ⅱ)图②能盖住三个正方形所需的圆形硬纸板最小直径为 cm;
(Ⅲ)图③能盖住三个正方形所需的圆形硬纸板最小直径为 cm;
(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法,(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com