Question

三角形两边的长分别是8和6，第3边的长是一元二次方程x²-16x+60=0的一个实数根，则该三角形的面积是________．

Answer 1

24或8
分析：由x²-16x+60=0，可利用因式分解法求得x的值，然后分别从x=6时，是等腰三角形；与x=10时，是直角三角形去分析求解即可求得答案．
解答：解：∵x²-16x+60=0，
∴（x-6）（x-10）=0，
解得：x₁=6，x₂=10，
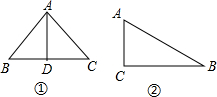
当x=6时，则三角形是等腰三角形，如图①：AB=AC=6，BC=8，AD是高，
∴BD=4，AD==2，
∴S_△ABC=BC•AD=×8×2=8；
当x=10时，如图②，AC=6，BC=8，AB=10，
∵AC²+BC²=AB²，
∴△ABC是直角三角形，∠C=90°，
S_△ABC=BC•AC=×8×6=24．
∴该三角形的面积是：24或8．
故答案为：24或8．
点评：此题考查了一元二次方程的解法、等腰三角形的性质与直角三角形的性质．此题难度适中，解题的关键是注意分类讨论思想，小心别漏解．