
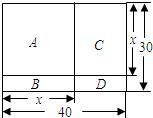
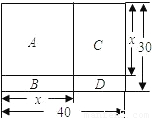
现有一块矩形场地,如图所示,长为40 m,宽为30 m,要将这块地划分为四块,分别种植:
A.兰花;B.菊花;C.月季;D.牵牛花.

(1)求出这块场地中种植菊花的面积y与B场地的长x之间的函数关系式;求出此函数与x轴的交点坐标,并写出自变量的取值范围.
(2)当x是多少时,种植菊花的面积最大?最大面积是多少?请画出此函数图象的草图(提示:找三点描出图象即可).
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
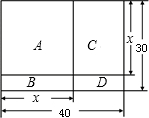 兰花;B.菊花;C.月季;D.牵牛花.且A为正方形.
兰花;B.菊花;C.月季;D.牵牛花.且A为正方形.| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:青海省中考真题 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(20):2.6 何时获得最大利润(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第27章《二次函数》中考题集(23):27.3 实践与探索(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com