
长方形的一边长等于3a+2b,另一边比它大a﹣b,那么这个长方形的周长是( )
A. 14a+6b B. 7a+3b C. 10a+10b D. 12a+8b
A 【解析】由题意知,长方形的另一边长等于(3a+2b)+(a﹣b)=3a+2b+a﹣b=4a+b, 所以这个长方形的周长是2(3a+2b+4a+b)=2(7a+3b)=14a+6b, 故选A.科目:初中数学 来源:2017-2018学年江苏苏州姑苏区第十中学初二上期中试卷数学试卷 题型:解答题
在直角坐标系中,一条直线经过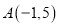 ,
, 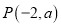 ,
, 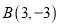 三点.
三点.
(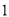 )求
)求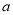 的值.
的值.
(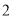 )设这条直线与
)设这条直线与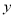 轴相交于点
轴相交于点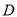 ,求
,求 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:江苏省2018届九年级上学期期末模拟数学试卷 题型:单选题
如图,点A、B、 C 、D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C 、D 、E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
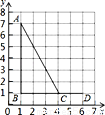
A. (4,2) B. (6,0) C. (6,3) D. (6,5)
C 【解析】试题分析:∵点A、B、C的坐标分别是(1,7),(1,1),(4,1), ∴AB=6,BC=3,∠ABC=90°, 当E点坐标为(4,2),而D(6,1),则CE=1,CD=2,∠ECD=90°, ∵=3,∠ABC=∠ECD, ∴△ABC∽△DCE; 当E点坐标为(6,0),而D(6,1),则ED=1,CD=2,∠EDC=90°, ∵=3,∠A...查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年七年级上期末模拟数学试卷 题型:填空题
小明买了20本练习本,店主给他八折优惠,结果便宜1.6元,每本练习本的标价是________元 .
0.4 【解析】试题解析:设每本练习本的标价是x元. 则 20×(1-0.8)x=1.6, 解得: x=0.4. 故答案为:0.4.查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年七年级上期末模拟数学试卷 题型:单选题
绝对值最小的有理数是( )
A. -1 B. 0 C. 1 D. 不存在
B 【解析】试题解析:0是绝对值最小的有理数. 故选B.查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市中考数学模拟试卷 题型:解答题
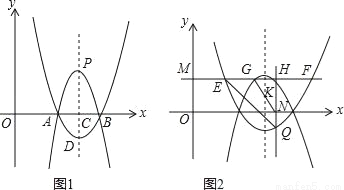
如图1,二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),其对称轴l与x轴交于点C,它的顶点为点D.
(1)写出点D的坐标 .
(2)点P在对称轴l上,位于点C上方,且CP=2CD,以P为顶点的二次函数y2=ax2+bx+c(a≠0)的图象过点A.
①试说明二次函数y2=ax2+bx+c(a≠0)的图象过点B;
②点R在二次函数y1=(x﹣2)(x﹣4)的图象上,到x轴的距离为d,当点R的坐标为 时,二次函数y2=ax2+bx+c(a≠0)的图象上有且只有三个点到x轴的距离等于2d;
③如图2,已知0<m<2,过点M(0,m)作x轴的平行线,分别交二次函数y1=(x﹣2)(x﹣4)、y2=ax2+bx+c(a≠0)的图象于点E、F、G、H(点E、G在对称轴l左侧),过点H作x轴的垂线,垂足为点N,交二次函数y1=(x﹣2)(x﹣4)的图象于点Q,若△GHN∽△EHQ,求实数m的值.
查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市中考数学模拟试卷 题型:解答题
计算: 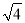 ﹣(π﹣2016)0+|
﹣(π﹣2016)0+|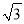 ﹣2|+2sin60°.
﹣2|+2sin60°.
查看答案和解析>>
科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:解答题
已知:在平面直角坐标系中,抛物线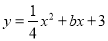 交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.
交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.
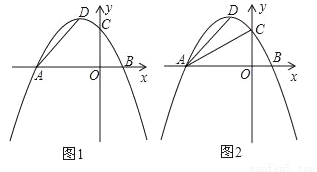
(1)求抛物线的解析式及顶点D的坐标.
(2)如图1,当0≤t≤4时,设△PAD的面积为S,求出S与t之间的函数关系式;S是否有最小值?如果有,求出S的最小值和此时t的值.
(3)如图2,当点P运动到使∠PDA=90°时,Rt△ADP与Rt△AOC是否相似?若相似,求出点P的坐标;若不相似,说明理由.
(1),顶点D的坐标为(﹣2,4);(2)S=﹣2t+12,当t=4时,S有最小值4;(3)相似,P的坐标为(0,2). 【解析】(1)对称轴为x=﹣=﹣2, 解得b=﹣1, 所以,抛物线的解析式为y=﹣x2﹣x+3, ∵y=﹣x2﹣x+3=﹣(x+2)2+4, ∴顶点D的坐标为(﹣2,4); (2)令y=0,则﹣x2﹣x+3=0, 整理得,x2+4x﹣1...查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级上期末模拟数学试卷 题型:单选题
三角形的三边长a,b,c满足2ab=(a+b)2﹣c2,则此三角形是( )
A. 钝角三角形 B. 锐角三角形 C. 直角三角形 D. 等边三角形
C 【解析】∵原式可化为a2+b2=c2 , ∴此三角形是直角三角形, 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com