解:
(1)将A(-1,0)、(0,-3)代入y=ax
2-2ax+b中,
得到:a=1,b=-3
∴所求二次函数的解析式为:y=x
2-2x-3.
(2)易求:C(1,-4)B(3,0)
BC:y=2x-6
BD:y=-2x+6关于x轴对称
从而∠DBA=∠CBA
①若:△ABD∽△PBC则:

=
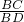
设P(k,0),则PB=3-K而BC=

,BD=

,AB=4
从而K=

,此时P(

,0).
②若:△ABD∽△CBP则:
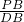
=

,易知:k=-12
此时P(-12,0).
③若:△ABD∽△BCP则:∠BCP=∠ABD=∠ABC
从而:AB∥CP而P点在x轴上,故这种情况不成立.
综上所述:符合条件的P点坐标是P(

,0)或P(-12,0).
分析:(1)将已知的抛物线上两点的坐标代入抛物线中进行求解即可.
(2)本题要分类进行讨论:
①当△ABD∽△PBC时,可得出关于PB、AB、BC、BD的比例关系式,可设出P点的横坐标,然后表示出PB的长,而BC,BD的长可根据B、C、D三点的坐标求得,因此根据此比例关系式即可求出P点的坐标.
②当△ABD∽△CBP时,同①
③当△ABD∽△BCP时,此时∠ABD=∠BCP,AB∥PC,显然是不成立的.
点评:本题考查了二次函数解析式的确定、相似三角形的判定和性质等知识点.
(2)在不确定相似三角形的对应角和对应边的情况下要分类讨论,不要漏解.

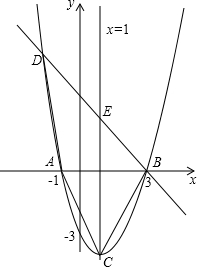 点B在A点的右侧;交y轴于(0,-3).
点B在A点的右侧;交y轴于(0,-3). =
=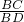
 ,BD=
,BD= ,AB=4
,AB=4 ,此时P(
,此时P( ,0).
,0).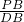 =
= ,易知:k=-12
,易知:k=-12 ,0)或P(-12,0).
,0)或P(-12,0).

 导学全程练创优训练系列答案
导学全程练创优训练系列答案
 如图,在平面直角坐标中,已知直线y=kx+b与直线y=
如图,在平面直角坐标中,已知直线y=kx+b与直线y= 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=