
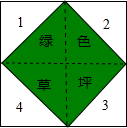
 如图所示,一个大正方形地面上,编号为1,2,3,4的地块,是四个全等的等腰直角三角形空地,中间是小正方形绿色草坪,一名训练有素的跳伞运动员,每次跳伞都能落在大正方形地面上.
如图所示,一个大正方形地面上,编号为1,2,3,4的地块,是四个全等的等腰直角三角形空地,中间是小正方形绿色草坪,一名训练有素的跳伞运动员,每次跳伞都能落在大正方形地面上.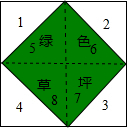 解:(1)根据题意得:如图,将大正方形分成8块全等等腰直角三角形,
解:(1)根据题意得:如图,将大正方形分成8块全等等腰直角三角形, ; …
; …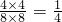 .…
.…

科目:初中数学 来源: 题型:
| 3 |
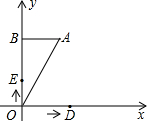 长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒.
长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:022
如图所示,取一个小立方块作为基本单元(图①),将10个基本单元排成一个“长条”(图②),再用10个“长条”组成一个长方体(图③),最后用10个长方体构成一个正方本(图④).
(1)如图③所示的长方体由 个小立方块组成.
(2)构成图④所示的正方体,需要 个小立方块.
(3)用图④所示的正方体作为新的基本单元,重复上述过程,得到一个更大的正方体,这个正方体至少需要 个小立方块.

查看答案和解析>>
科目:初中数学 来源:2011届河南省平顶山市第二次中考模拟考试数学试卷 题型:解答题
(11分)如图1,已知抛物线经过原点0和x轴上另一个点E,顶点M的坐标是(2,4); 矩形ABCD的顶点A与点0重合,AD、AB分别在x轴和y轴上,且AD="2" ,AB=3.
(1)求该抛物线所参应的函数表达式;
(2)将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2).
①当t= 时,判断点P时否在直线ME上,并说明理由;
时,判断点P时否在直线ME上,并说明理由;
②设以P、N、C、D为顶点的图形面积为S,试部S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.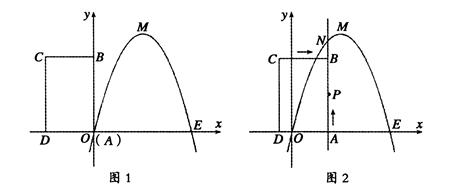
查看答案和解析>>
科目:初中数学 来源:2010-2011学年河南省平顶山市考模拟考试数学试卷 题型:解答题
(11分)如图1,已知抛物线经过原点0和x轴上另一个点E,顶点M的坐标是(2,4); 矩形ABCD的顶点A与点0重合,AD、AB分别在x轴和y轴上,且AD=2 ,AB=3.
(1)求该抛物线所参应的函数表达式;
(2)将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2).
①当t= 时,判断点P时否在直线ME上,并说明理由;
时,判断点P时否在直线ME上,并说明理由;
②设以P、N、C、D为顶点的图形面积为S,试部S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:浙江省月考题 题型:解答题
 个单位长度的速度沿x轴正方向运动,E点以每秒1个单位长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒。
个单位长度的速度沿x轴正方向运动,E点以每秒1个单位长度的速度沿y轴正方向运动,设D、E两点的运动时间为t秒。 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com