
点C在线段AB上,以AC和BC为边在AB的同侧作正△ACM和正△BCN(如图),连结AN、BM分别交CM、CN于点P、G.求证:PG∥AB.

|
证明:∵△ ACM和△BCN分别是等边三角形,∴∠ 1=∠3=∠6=∴∠ 1+∠3=∠3+∠6=即∠ ACN=∠BCM.又∵ AC=CM,BC=CN,∴△ ACN≌△MCB.∴∠ 5=∠4.又∵∠ 1=∠3=∴△ PCN≌△GCB.∴ PC=GC.又∵∠ 3=∴△ PCG是等边三角形.∴∠ 2=又∠ 1=∴∠ 1=∠2.∴ PG∥AB. |
|
点悟:要证 PG∥AB,需证∠1=∠2.而由△ACM和△BCN为等边三角形知∠3=点拨:本例中先证的△ ACN和△BCM全等,主要是为第二对三角形(△PCN和△GCB)全等的证明创造条件. |


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
 如图,点C在线段AB上,以AB、AC为直径的半圆相切于点A,大圆的弦AE交小圆于点D,∠EAB=α,如DE=2,那么BC等于( )
如图,点C在线段AB上,以AB、AC为直径的半圆相切于点A,大圆的弦AE交小圆于点D,∠EAB=α,如DE=2,那么BC等于( )| A、2cosα | ||
| B、2sinα | ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
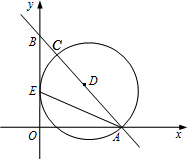 如图,在平面直角坐标系中,直线y=-
如图,在平面直角坐标系中,直线y=-| 4 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
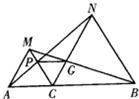 25、如图,已知点C在线段AB上,以AC和BC为边在AB同侧作正△ACM和正△BCN,连接AN,BM,分别交CM,CN于点P,G,连接PG.求证:PG∥AB.
25、如图,已知点C在线段AB上,以AC和BC为边在AB同侧作正△ACM和正△BCN,连接AN,BM,分别交CM,CN于点P,G,连接PG.求证:PG∥AB.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
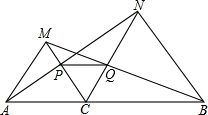 已知:如图,点C在线段AB上,以AC和BC为边在AB的同侧作正三角形△ACM和△BCN,连接AN、BM,分别交CM、CN于点P、Q.求证:PQ∥AB.
已知:如图,点C在线段AB上,以AC和BC为边在AB的同侧作正三角形△ACM和△BCN,连接AN、BM,分别交CM、CN于点P、Q.求证:PQ∥AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com