已知函数y=mx2-3x+2(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若一次函数y=x+1的图象与该函数的图象恰好只有一个交点,求m的值 及这个交点的坐标.
解:(1)当m=0时,函数为一次函数,
令x=0,
则y=2,该函数的图象都经过y轴上的一个定点(0,2);
当m≠0时,函数为二次函数,
当x=0时,y=2,该函数图象过y轴上一个定点(0,2).
可见,不论m为何值,该函数的图象都经过y轴上的一个定点.
(2)当m=0时,两函数均为一次函数且比例系数不同,必有一交点,列方程组得

;
解得
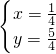
,即交点坐标为(

,

);
当m≠0时,把y=x+1代入y=mx
2-3x+2得,x+1=mx
2-3x+2,整理得mx
2-4x+1=0,
∵两函数图象只有一个交点;
∴△=0,即△=(-4)
2-4m=0.
解得m=4,
把m=4代入方程mx
2-4x+1=0得,4x
2-4x+1=0,解得x=

,
把x=

代入一次函数y=x+1得,y=

+1=

,即两函数交点坐标为(

,

).
故当m=0时,两函数交点坐标为(

,

);
当m=4时,两函数交点坐标为(

,

).
分析:(1)分两种情况讨论:
当m=0时,函数为一次函数,由于求证点在y轴上,令x=0,可求出图象与y轴的交点;
当m≠0时,函数为二次函数,由于求证点在y轴上,令x=0,可求出图象与y轴的交点.然后验证该两点为同一点即可.
(2)当m=0时,两函数均为一次函数,必有一交点; 当m≠0时函数为二次函数,将两函数组成方程组,转化为一元二次方程,利用根的判别式求m的值即可.
点评:本题考查的是二次函数的性质、二次函数图象上点的坐标特点及根的判别式,在解答此题时要注意分类讨论,不要漏解.

 ;
;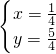 ,即交点坐标为(
,即交点坐标为( ,
, );
); ,
, 代入一次函数y=x+1得,y=
代入一次函数y=x+1得,y= +1=
+1= ,即两函数交点坐标为(
,即两函数交点坐标为( ,
, ).
). ,
, );
); ,
, ).
).

 全优点练单元计划系列答案
全优点练单元计划系列答案