
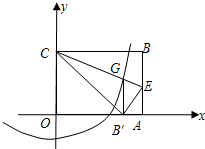
如图,在直角坐标系xOy中,点A在x轴的正半轴上,点B在y轴的正半轴上, 以OB为直径的⊙C与AB交于点D, DE与⊙C相切交x轴于点E, 且 OA= cm,∠OAB=30°.
cm,∠OAB=30°.
(1)求点B的坐标及直线AB的解析式;
(2)过点B作BG^EC于 F, 交x轴于点G, 求BD的长及点F的坐标;
(3)设点P从点A开始沿A B
B G的方向以4cm/s的速度匀速向点G移动,点Q同时
G的方向以4cm/s的速度匀速向点G移动,点Q同时
从点A开始沿AG匀速向点G移动, 当四边形CBPQ为平行四边形时, 求点Q的移动
 速度.
速度.
解:(1)由OA^ OB, ∠OAB=30°, OA= ,可得AB=2OB.
,可得AB=2OB.
在Rt△AOB中, 由勾股定理得OB=12,AB=24.
∴ B(0, 12). …………………………………………1分
∵ OA= ,
,
∴ A ( ,0).
,0).
可得直线AB的解析式为 .
……………………2分
.
……………………2分
(2)法一: 连接CD, 过F作FM⊥x轴于点M,则CB=CD.
连接CD, 过F作FM⊥x轴于点M,则CB=CD.
∵ ∠OBA=90°-∠A=60°,
∴ △CBD是等边三角形.
∴
BD=CB= OB=6,
……………………3分
OB=6,
……………………3分
∠BCD=60°, ∠OCD=120°.
∵ OB是直径,OA^ OB,
∴ OA切⊙C于O.
∵ DE切⊙C于D,
∴ ∠COE=∠CDE=90°, ∠OEC=∠DEC.
∴ ∠OED=360° -∠COE-∠CDE -∠OCD = 60°.
∴ ∠OEC=∠DEC=30°.
∴ CE=2 CO=12.
∴ 在Rt△COE中, 由勾股定理OE= . ……………………4分
. ……………………4分
∵ BG^EC于F,
∴ ∠GFE=90°.
∵ ∠GBO +∠BGO=∠OEC +∠BGO ,
∴ ∠GBO=∠OEC =30°.
故可得FC= BC=3, EF=FC+CE=15,
BC=3, EF=FC+CE=15,
FM= EF=
EF= , ME=
, ME= FM=
FM= ………………………………………5分
………………………………………5分
∴ MO=
 ∴ F(
∴ F( ,
, ).
………………………………………6分
).
………………………………………6分
法二:连接OD, 过D作DH^ OB于H.
∵ OB是直径,
∴ ∠BDO=90°.
∵∠BOD +∠DOA=∠A +∠DOA,
∴ ∠BOD=∠A =30°.
由(1)OB=12,
∴  ……………………………………………………3分
……………………………………………………3分
在Rt△DOB中, 由勾股定理得 OD= .
.
在Rt△DOH中, 由勾股定理得 HD= , OH=9.
, OH=9.
∴ D( ,
9).
,
9).
可得直线 OD的解析式为 
由BG//DO, B(0, 12),
可得直线BG的解析式为  ……………………………………4分
……………………………………4分
∵ OB是直径,OA^ OB,
∴ OA切⊙C于O.
∵ DE切⊙C于D,
∴ EO=ED.
∵ ∠DOE=∠BOA -∠BOD =60°,
∴ △ODE是等边三角形.
∴  .
.
∴
EA=OA- OE= .
.
∵
OC=CB=6, OE=EA= ,
,
∴ C(0, 6), CE//BA.
∴ 直线CE的解析式为  ………………………………………5分
………………………………………5分
由 
∴ F( ,
, ).
……………………………………………………6分
).
……………………………………………………6分
(3)设点Q移动的速度为vcm/s .
(ⅰ)当点P运动到AB中点,点Q运动到AO中点时,
PQ∥BC,且PQ=BC,此时四边形CBPQ为平行四边形, 点Q与点E重合.

∴ (cm/s).
………………………………………7分
(cm/s).
………………………………………7分
 (ⅱ) 当点P运动到BG中点,点Q运动到OG中点时,
(ⅱ) 当点P运动到BG中点,点Q运动到OG中点时,
PQ∥BC,PQ=BC, 此时四边形CBPQ为平行四边形.
可得 BG=
BG= 从而PB=
从而PB= ,OQ=
,OQ=
∴ 
∴  (cm/s). (分母未有理化不扣分) ………8分
(cm/s). (分母未有理化不扣分) ………8分
∴ 点Q的速度为 cm/s或
cm/s或 cm/s.
cm/s.
【解析】略


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
 是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.
是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 4 |
| 1 |
| 8 |
| 14 |
| 3 |
 半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.查看答案和解析>>
科目:初中数学 来源: 题型:
 已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.
已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.
如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.查看答案和解析>>
科目:初中数学 来源: 题型:
| a+2 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com