
| 如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点. |
 |
| (1)求抛物线的解析式. (2)已知AD = AB(D在线段AC上),有一动点P从点A沿线段AC以每秒1个单位长度的速度移动;同时另一个动点Q以某一速度从点B沿线段BC移动,经过t 秒的移动,线段PQ被BD垂直平分,求t的值; (3)在(2)的情况下,抛物线的对称轴上是否存在一点M,使MQ+MC的值最小?若存在,请求出点M的坐标;若不存在,请说明理由。 |
|
(1)设抛物线的解析式为y = a (x +3 )(x - 4),因为B(0,4)在抛物线上, 所以4 = a ( 0 + 3 ) ( 0 - 4 )解得,  所以抛物线解析式为  ; ;(2) 连接DQ,在Rt△AOB中,  ,所以AD=AB= 5, ,所以AD=AB= 5,PQ⊥BD,所以∠PDB=∠QDB因为AD=AB,所以∠ABD=∠ADB,∠ABD=∠QDB,所以 DQ∥AB,所以∠CQD=∠CBA。∠CDQ=∠CAB,所以△CDQ∽ △CAB,  即 即 所以AP=AD - DP = AD - DQ=5 - 所以AP=AD - DP = AD - DQ=5 - = = , , 所以t的值是  ; ;(3)对称轴上存在一点M,使MQ+MC的值最小. 理由:因为抛物线的对称轴为  所以A(- 3,0),C(4,0)两点关于直线  对称.连接AQ交直线 对称.连接AQ交直线 于点M,则MQ+MC的值最小.过点Q作QE⊥x轴,于E,所以∠QED=∠BOA=90° DQ∥AB,∠ BAO=∠QDE,∴△DQE ∽△ABO.  即  ,所以QE= ,所以QE= ,DE= ,DE= ,所以OE = OD + DE=2+ ,所以OE = OD + DE=2+ = = , ,所以Q(  , , ). ). 设直线AQ的解析式为  则 则  所以直线AQ的解析式为  联立 联立  由此得   则:在对称轴上存在点M  ,使MQ+MC的值最小. ,使MQ+MC的值最小. |


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
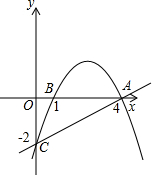 如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.
如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点,
如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点,查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•苏州一模)如图,抛物线经过A,C,D三点,且三点坐标为A(-1,0),C(0,5),D(2,5),抛物线与x轴的另一个交点为B点,点F为y轴上一动点,作平行四边形DFBG,
(2013•苏州一模)如图,抛物线经过A,C,D三点,且三点坐标为A(-1,0),C(0,5),D(2,5),抛物线与x轴的另一个交点为B点,点F为y轴上一动点,作平行四边形DFBG,5-
| ||
| 5 |
5+
| ||
| 5 |
5-
| ||
| 5 |
5+
| ||
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•高要市二模)已知:如图,抛物线经过点O、A、B三点,四边形OABC是直角梯形,其中点A在x轴上,点C在y轴上,BC∥OA,A(12,0)、B(4,8).
(2013•高要市二模)已知:如图,抛物线经过点O、A、B三点,四边形OABC是直角梯形,其中点A在x轴上,点C在y轴上,BC∥OA,A(12,0)、B(4,8).查看答案和解析>>
科目:初中数学 来源: 题型:
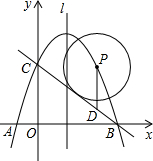 如图,抛物线经过A(-2,0)、B(8,0)两点,与y轴正半轴交与点C,且AB=BC,点P为第一象限内抛物线上一动点(不与B、C重合),设点P的坐标为(m,n).
如图,抛物线经过A(-2,0)、B(8,0)两点,与y轴正半轴交与点C,且AB=BC,点P为第一象限内抛物线上一动点(不与B、C重合),设点P的坐标为(m,n).| BD•DC | PD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com