
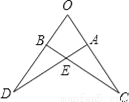
如图,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD=__度.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:北京市顺义区2018届初三上学期期末考试数学试卷 题型:解答题
如图,在平面直角坐标系xOy中,直线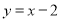 与双曲线
与双曲线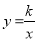 (k≠0)相交于A,B 两点,且点A的横坐标是3.
(k≠0)相交于A,B 两点,且点A的横坐标是3.
(1)求k的值;
(2)过点P(0,n)作直线,使直线与x轴平行,直线与直线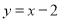 交于点M,与双曲线
交于点M,与双曲线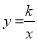 (k≠0)交于点N,若点M在N右边,求n的取值范围.
(k≠0)交于点N,若点M在N右边,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年陕西安市九年级(上)期末数学试卷 题型:单选题
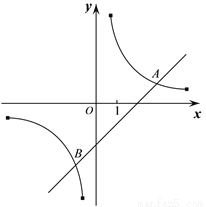
二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
B 【解析】 试题分析:根据抛物线的对称轴为直线x=﹣=2,则有4a+b=0;观察函数图象得到当x=﹣3时,函数值小于0,则9a﹣3b+c<0,即9a+c<3b;由于x=﹣1时,y=0,则a﹣b+c=0,易得c=﹣5a,所以8a+7b+2c=8a﹣28a﹣10a=﹣30a,再根据抛物线开口向下得a<0,于是有8a+7b+2c>0;由于对称轴为直线x=2,根据二次函数的性质得到当x>2时...查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:解答题
某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.该商场两次共购进这种运动服多少套?
该商场两次共购进这种运动服600套. 【解析】试题分析:设第一次购进x套,则第二次购进2x套,第一批购进数量为,第二批购进数量为,根据题意列出方程+10=,解出x并验证是否为增根. 试题解析: 【解析】 设第一次购进x套,则第二次购进2x套, ,解得 x=200, 经检验x=200是方程的解. 200+200×2=600. 答:该商场两次共购进这种运动服...查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:填空题
已知关于x的分式方程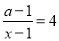 的解为非负数,则a的取值范围是_____________.
的解为非负数,则a的取值范围是_____________.
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:单选题
下列各式中,正确的是( )
A. 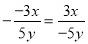 B.
B. 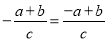
C. 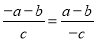 D.
D. 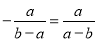
查看答案和解析>>
科目:初中数学 来源:北京市分校2017-2018学年度第一学期期中初二数学试卷 题型:解答题
阅读下列材料
通过小学的学习我们知道,分数可分为“真分数”和“假分数”.而假分数都可化为带分数,如: 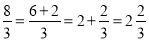 .
.
我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
如: 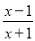 ,
, 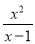 这样的分式就是假分式;再如:
这样的分式就是假分式;再如: 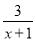 ,
, 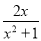 这样的分式就是真分式.
这样的分式就是真分式.
类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).
如: 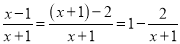 ;
; 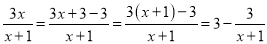 ;
;
再如: 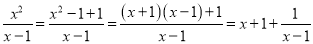 .
.
解决下列问题:
(1)分式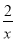 是 分式(填“真分式”或“假分式”);
是 分式(填“真分式”或“假分式”);
(2)假分式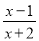 可化为带分式 的形式;
可化为带分式 的形式;
(3)如果分式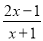 的值为整数,那么x的整数值为 .
的值为整数,那么x的整数值为 .
查看答案和解析>>
科目:初中数学 来源:北京市分校2017-2018学年度第一学期期中初二数学试卷 题型:单选题
如图,有一池塘,要测池塘两端A、B两点的距离,可先在平地上取一个可以直接到达A、B两点的C,连接AC并延长AC到点D,使CD=CA,连结BC并延长BC到点E,使CE=CB,连接DE,那么量出DE的长就等于AB的长, 这是因为可根据 (简写)方法判定△ABC≌△DEC.
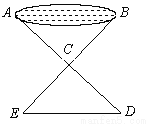
A. SSS B. SAS C. AAS D. ASA
B 【解析】如图,连接AB, 由题意可知,在△ABC和△DCE中, , ∴△ABC≌△DCE(SAS). 故选B.查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
如图,在△ABC中,∠C=90°,BC=6,AC=9,将△ABC平移使其顶点C位于△ABC的重心G处,则平移后所得三角形与原△ABC的重叠部分面积是_____.
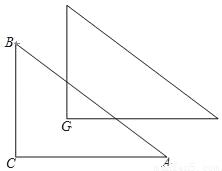
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com