
阅读下列材料:
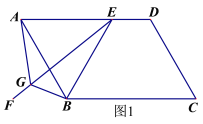
问题:如图1,在平行四边形ABCD中,E是AD上一点,AE=AB,∠EAB=60°,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
求证:EG =AG+BG.
小明同学的思路是:作∠GAH=∠EAB交GE于点H,构造全等三角形,经过推理解决问题.
参考小明同学的思路,探究并解决下列问题:
(1)完成上面问题中的证明;
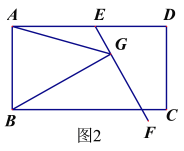
(2)如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”,原问题中的其它条件不变(如图2),请探究线段EG、AG、BG之间的数量关系,并证明你的结论.
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源:北京市2017-2018学年七年级第二学期期中考试数学试卷 题型:解答题
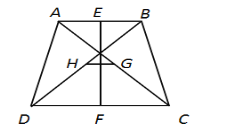
如图,在四边形ABCD中,AB∥CD,AB≠CD,BD=AC.
(1)求证:AD=BC;
(2)若E,F,G,H分别是AB,CD,AC,BD的中点,求证:线段EF与线段GH互相垂直平分.
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年七年级第二学期期中考试数学试卷 题型:填空题
已知命题:“如果两个三角形全等,那么这两个三角形的面积相等.”写出它的逆命题:_______________________________,该逆命题是________(填“真”或“假”)命题.
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年七年级第二学期期中考试数学试卷 题型:单选题
如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AB,BC边上的中点,连接EF.若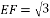 ,BD=4,则菱形ABCD的周长为( )
,BD=4,则菱形ABCD的周长为( )
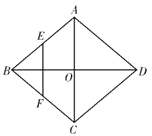
A. 4 B. 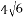 C.
C. 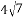 D. 28
D. 28
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年度第二学期期中考试八年级数学试卷 题型:解答题
已知关于
 有两个不相等的实数根.
有两个不相等的实数根.
(1)求
(2)若

查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年度第二学期期中考试八年级数学试卷 题型:填空题
如图,将矩形ABCD沿对角线BD所在直线折叠,点C落在同一平面内,落点记为C’,BC’与AD交于点E,若 AB=3,BC=4,则DE的长为_______________.
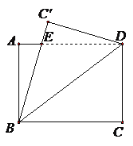
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com