
 .例如f(15)=3×15+1=46,
.例如f(15)=3×15+1=46, .若a1=8,a2=f(a1),a3=f(a2),a4=f(a3),…,依此规律进行下去,得到一列数a1,a2,a3,a4,…,an,…(n为正整数),则a3=________,a1+a2+a3+…+a2014=________.
.若a1=8,a2=f(a1),a3=f(a2),a4=f(a3),…,依此规律进行下去,得到一列数a1,a2,a3,a4,…,an,…(n为正整数),则a3=________,a1+a2+a3+…+a2014=________. 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
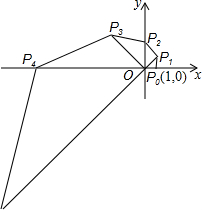 如图,在直角坐标系中,已知点P0的坐标为(1,0),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数).我们规定:把点Pn(xn,yn)(n=0,1,2,3,…)的横坐标xn、纵坐标yn都取绝对值后得到的新坐标(|xn|,|yn|)称之为点Pn的“绝对坐标”.则Pn的“绝对坐标”为( )
如图,在直角坐标系中,已知点P0的坐标为(1,0),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数).我们规定:把点Pn(xn,yn)(n=0,1,2,3,…)的横坐标xn、纵坐标yn都取绝对值后得到的新坐标(|xn|,|yn|)称之为点Pn的“绝对坐标”.则Pn的“绝对坐标”为( )A、(2n-1
| ||||
| B、(2n,0)或(0,2n) | ||||
C、(0,2n)或(2n-1
| ||||
D、(2n-1
|
查看答案和解析>>
科目:初中数学 来源:2012年浙江省杭州市文澜中学中考数学模拟试卷(解析版) 题型:选择题

 ,
, )或(2n,0)
)或(2n,0) ,
, )
) ,
, )或(2n,0)或(0,2n)
)或(2n,0)或(0,2n)查看答案和解析>>
科目:初中数学 来源:2010年湖北省天门市石河中学中考数学模拟试卷7(解析版) 题型:选择题

 ,
, )或(2n,0)
)或(2n,0) ,
, )
) ,
, )或(2n,0)或(0,2n)
)或(2n,0)或(0,2n)查看答案和解析>>
科目:初中数学 来源:2010年浙江省杭州市文澜中学中考数学模拟试卷(解析版) 题型:选择题

 ,
, )或(2n,0)
)或(2n,0) ,
, )
) ,
, )或(2n,0)或(0,2n)
)或(2n,0)或(0,2n)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com