
| 3 |
| 4 |

| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
|


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| x | -3 | -2 | 0 | 1 | 2 | 3 | 5 |
| y | 7 | 0 | -8 | -9 | m | -5 | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•宽城区一模)某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图①所示,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30cm.如图②,当∠BAC=18°时,CD⊥AB于D,求支撑臂CD的长.
(2012•宽城区一模)某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图①所示,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30cm.如图②,当∠BAC=18°时,CD⊥AB于D,求支撑臂CD的长.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
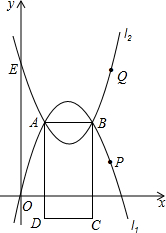 有两条抛物线l1、l2都经过A、B两点,且关于AB所在直线对称,其中抛物线l1经过原点,抛物线l2交y轴于点E.设P、Q两点分别在抛物线l1、l2上运动.
有两条抛物线l1、l2都经过A、B两点,且关于AB所在直线对称,其中抛物线l1经过原点,抛物线l2交y轴于点E.设P、Q两点分别在抛物线l1、l2上运动.| 1 |
| 5 |
| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com