
已知△ABC是等腰直角三角形,∠A=90° ,D是腰AC上的一个动点,过C作CE垂直于BD或BD的延长线,垂足为E,如图.

(1)若BD是AC的中线,求![]() 的值;
的值;
(2)若BD是∠ABC的角平分线,求![]() 的值;
的值;
(3)结合(1)、(2),试推断![]() 的取值范围(直接写出结论,不必证明),并探究
的取值范围(直接写出结论,不必证明),并探究![]() 的值能小于
的值能小于![]() 吗?若能,求出满足条件的D点的位置;若不能,说明理由.
吗?若能,求出满足条件的D点的位置;若不能,说明理由.
|
解法1:设AB=AC=1,CD=x,则0<x<1,BC= 在Rt△ABD中,BD2=AB2+AD2=1+(1-x)2=x2-2x+2. 由已知可得Rt△ABD∽Rt△ECD, ∴ ∴ (1)若BD是AC的中线,则CD=AD=x= (2)若BD是∠ABC的角平分线,则 ∴ (3)若 ∴ 解法2:设AB=AC=1,∠ABD=a
,则BC= 在Rt△ABD中,有 在Rt△BCE中,有CE=BC·sin∠CBE= 因此 解法3:(1)∵∠A=∠E=90°
,∠ADB=∠CDE,∴△ADB∽△EDC,∴ 由于D是中点,且AB=AC,知AB=2AD,于是CE=2DE. 在Rt△ADB中,BD= 在Rt△CDE中,由CE2+DE2=CD2,有CE2+ 而AD=CD,所以 (2)如图少图,延长CE、BA相交于点F.∵BE是∠ABC的平分线,且BE⊥CF,∴△CBE≌△FBE,得CE=EF,于是CF=2CE.又∠ABD+∠ADB=∠CDE+∠FCA=90° ,且∠ADB=∠CDE, ∴∠ABD=∠FCA,进而有△ABD≌△ACF,得BD=2CE, (3) |


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 3 |
| 3 |
| 5 |
2-2
|
2-2
|
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.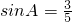 ,其中A为锐角,试求sadA的值;
,其中A为锐角,试求sadA的值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com