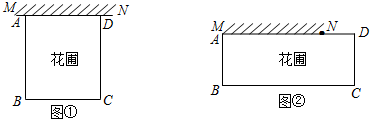
15.甲、乙、丙、丁四人利用一段旧直墙MN与长为32m的篱笆共同围成一个外形为矩形的花圃.已知原旧直墙MN的最大可利用长度为8m,求围成的花圃的最大面积.
甲的方案:如图①,设BC=xm,围成的花圃面积为Sm
2,则
S=x•$\frac{32-x}{2}$=$-\frac{1}{2}{({x-16})^2}+128$,当x=16时,围成的花圃的面积最大为128m
2;
乙的方案:如图①,设BC=xm,围成的花圃面积为Sm
2,则
S=x•$\frac{32-x}{2}$=$-\frac{1}{2}{({x-16})^2}+128$,当x=8时,围成的花圃的面积最大为96m
2;
丙的方案:如图②,设BC=xm,围成的花圃面积为Sm
2,则
S=x•$\frac{40-2x}{2}$=-(x-10)
2+100,当x=8时,围成的花圃的面积最大为96m
2;
丁的方案:如图②,设BC=xm,围成的花圃面积为Sm
2,则
S=x•$\frac{40-2x}{2}$=-(x-10)
2+100,当x=10时,围成的花圃的面积最大为100m
2.
你认为求得的最大值应该是( )
| A. | 128m2 | | B. | 96m2 | | C. | 100m2 | | D. | 以上都不对 |

