
 和b4+b2-3=0,则代数式
和b4+b2-3=0,则代数式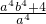 的值等于
的值等于 与b2为一元二次方程x2+x-3=0的两个根,利用根与系数的关系表示出两根之和与两根之积,把所求的式子先利用同分母分式的加法法则逆运算变形后,再利用完全平方公式变形,将得出的两根之和与两根之积代入,可得出所求式子的值.
与b2为一元二次方程x2+x-3=0的两个根,利用根与系数的关系表示出两根之和与两根之积,把所求的式子先利用同分母分式的加法法则逆运算变形后,再利用完全平方公式变形,将得出的两根之和与两根之积代入,可得出所求式子的值. 和b4+b2-3=0,
和b4+b2-3=0, -
- -3=0可化为:(-
-3=0可化为:(- )2+(-
)2+(- )-3=0,b4+b2-3=0可化为:(b2)2+b2-3=0,
)-3=0,b4+b2-3=0可化为:(b2)2+b2-3=0, 与b2为一元二次方程x2+x-3=0的两个根,
与b2为一元二次方程x2+x-3=0的两个根, +b2=-1,-
+b2=-1,- •b2=-3,
•b2=-3,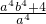 =b4+
=b4+ =(b2-
=(b2- )2+2•b2•
)2+2•b2• =(-1)2+6=7.
=(-1)2+6=7. ,x1x2=
,x1x2= .其中将已知的两等式适当变形后,得到-
.其中将已知的两等式适当变形后,得到- 与b2为一元二次方程x2+x-3=0的两个根是解本题的关键.
与b2为一元二次方程x2+x-3=0的两个根是解本题的关键. 

 口算能手系列答案
口算能手系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com