
已知Rt△ABC和Rt△EBC, °。以边AC上的点O为圆心、OA为半径的⊙O与EC相切,D为切点,AD//BC。
°。以边AC上的点O为圆心、OA为半径的⊙O与EC相切,D为切点,AD//BC。
(1)用尺规确定并标出圆心O;(不写做法和证明,保留作图痕迹)
(2)求证: [来源:Www.zk5u.com]
[来源:Www.zk5u.com]
(3)若AD=1, ,求BC的长。(8分)
,求BC的长。(8分)
(1)略
(2)略
(3)2
【解析】解:
(1)(提示:O即为AD中垂线与AC的交点或过D点作EC的垂线与AC的交点等).
能见作图痕迹,作图基本准确即可,漏标O可不扣分 2分
(2)证明:连结OD.∵AD∥BC , ∠B=90°,∴∠EAD=90°.

∴∠E+∠EDA=90°,即∠E=90°-∠EDA.
又圆O与EC相切于D点,∴OD⊥EC.
∴∠EDA+∠ODA=90°,即∠ODA=90°-∠EDA.[来源:Z_xx_k.Com]
∴∠E=∠ODA 3分
(说明:任得出一个角相等都评1分)
又OD=OA,∴∠DAC=∠ODA,∴∠DAC=∠E. 4分
∵AD∥BC,∴∠DAC=∠ACB,∴∠E=∠ACB. 5分
(3)Rt△DEA中,tan∠E= ,又tan∠E=tan∠DAC=
,又tan∠E=tan∠DAC= ,
,
∵AD=1∴EA= . 6分
. 6分
Rt△ABC中,tan∠ACB= ,
,
又∠DAC=∠ACB,∴tan∠ACB=tan∠DAC.
∴ =
= ,∴可设
,∴可设 .
.
∵AD∥BC,∴Rt△EAD∽Rt△EBC. 7分
∴ ,即
,即 .
.
∴ ,∴
,∴ . 8分
. 8分


科目:初中数学 来源: 题型:
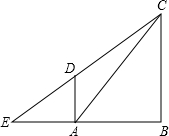 相切,D为切点,AD∥BC.
相切,D为切点,AD∥BC.
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
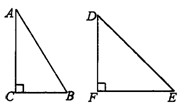 14、如图,已知Rt△ABC和Rt△DEF不相似,其中∠C,∠F为直角,∠A<∠D,能否分别将两个三角形分割成两个三角形,使△ABC所分的两个三角形与△DEF所分的两个三角形分别相似?如果能够,请设计一个分割方案;如果不能,请说明理由.
14、如图,已知Rt△ABC和Rt△DEF不相似,其中∠C,∠F为直角,∠A<∠D,能否分别将两个三角形分割成两个三角形,使△ABC所分的两个三角形与△DEF所分的两个三角形分别相似?如果能够,请设计一个分割方案;如果不能,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 2 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知Rt△ABC和三角形外一点P,按要求完成图形:
如图,已知Rt△ABC和三角形外一点P,按要求完成图形:查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com