
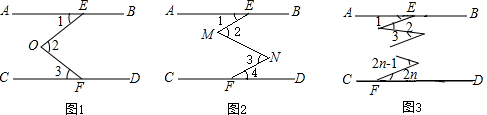
 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,下列结论一定成立的是( )
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,下列结论一定成立的是( )| A. | ∠A=∠1+∠2 | B. | 2∠A=∠1+∠2 | C. | 3∠A=2∠1+∠2 | D. | 3∠A=2(∠1+∠2) |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
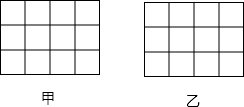 如图,正方形网格中的每个小正方形=边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图.
如图,正方形网格中的每个小正方形=边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届浙江省平阳县名校九年级下学期第一次模拟统练数学试卷(解析版) 题型:解答题
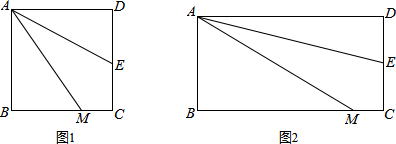
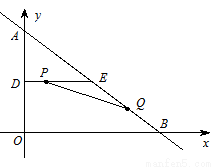
在平面直角坐标系中,直线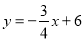 与
与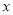 轴、
轴、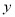 轴分别交于点B、 A,点D、E分别是AO、AB的中点,连接DE,点P从点D出发,沿DE方向匀速运动,速度为1cm/s;与此同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为
轴分别交于点B、 A,点D、E分别是AO、AB的中点,连接DE,点P从点D出发,沿DE方向匀速运动,速度为1cm/s;与此同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为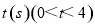 .
.
(1)分别写出点P和Q坐标(用含t的代数式表示);
(2)①当点Q在BE之间运动时,设五边形PQBOD的面积为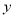 (cm2),求y与t之间的函数关系式;
(cm2),求y与t之间的函数关系式;
②在①的情况下,是否存在某一时刻t,使PQ分四边形BODE两部分的面积之比为S△PQE:S五边形PQBOD=1:29?若存在,求出此时t的值;若不存在,请说明理由;
(3)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,当t为何值时,⊙P能与△ABO的一边相切?
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com