
如图,将等腰△ABC绕顶点B逆时针方向旋转40°得到△A1BC1,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.
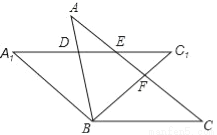
求证:ΔBCF≌ΔBA1D.
当∠C=40°时,请你证明四边形A1BCE是菱形.
(1)详见解析;(2)详见解析. 【解析】试题分析:(1)根据旋转的性质,得出A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBC1,再根据ASA即可判定△BCF≌△BA1D; (2)根据∠C=40°,△ABC是等腰三角形,即可得出∠A=∠C1=∠C=40°,进而得到∠C1=∠CBF,∠A=∠A1BD,由此可判定A1E∥BC,A1B∥CE,进而得到四边形A1BCE是平行四边形,... 口算能手系列答案
口算能手系列答案科目:初中数学 来源:2017年贵州省中考数学模拟试卷 题型:解答题
解分式方程: 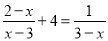 .
.
查看答案和解析>>
科目:初中数学 来源:浙江省金华市2017-2018学年八年级上册期末模拟数学试卷 题型:解答题
李老师每天坚持晨跑.下图反映的是李老师某天6:20从家出发小跑到赵化北门,在北门休息几分钟后又慢跑回家的函数图象. 其中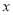 (分钟)表示所用时间,
(分钟)表示所用时间, 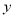 (千米)表示李欢离家的距离.
(千米)表示李欢离家的距离.
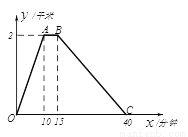
(1)分别求出线段0≤x≤10和15≤x≤40的函数解析式?
(2)李老师在这次晨跑过程中什么时间距离家500米?
(1)当0≤x≤10时,y=0.1x;当15≤x≤40时,y=3.2-0.08x; (2)李老师在这次晨跑过程中分别于5分、33.75分距离家500米。 【解析】试题分析:(1)利用待定系数法即可求得;(2)求出OA的解析式,然后根据OA、BC的解析式,利用y=0.5千米计算求出相应的x的值,再加上6点20分即可. 试题解析:(1)设OA的解析式为y1=kx, 则10k=2...查看答案和解析>>
科目:初中数学 来源:浙江省金华市2017-2018学年八年级上册期末模拟数学试卷 题型:单选题
如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD交BE于F,BF=AC,则∠ABC等于( )
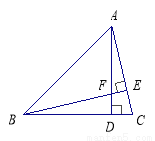
A.40° B.45° C.60° D.30°
B 【解析】∵AD⊥BC于D,BE⊥AC于E, ∴∠EAF+∠AFE=90°,∠DBF+∠BFD=90, 又∵∠BFD=∠AFE(对顶角相等), ∴∠EAF=∠DBF, 在Rt△ADC和Rt△BDF中, ∠EAF=∠DBF, ∠FDB=∠CDA, AC=BF ∴△ADC≌△BDF, ∴BD=AD, 即∠ABC=∠BAD=...查看答案和解析>>
科目:初中数学 来源:浙江省金华市2017-2018学年八年级上册期末模拟数学试卷 题型:单选题
如图,BD是∠ABC的角平分线,AD⊥AB,AD=3,BC=5,则△BCD的面积为( )
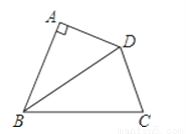
A. 7.5 B. 8 C. 10 D. 15
A 【解析】作DE⊥BC于E,根据角平分线的性质,由BD是∠ABC的角平分线,AD⊥AB,DE⊥BC,求出DE=DA=3,根据三角形面积公式计算S△BCD=×BC×DE=7.5, 故选:A.查看答案和解析>>
科目:初中数学 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:填空题
已知抛物线y=a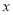 2+b
2+b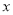 +c(a>0)的对称轴为直线
+c(a>0)的对称轴为直线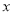 =1,且经过点(-1,y1)、(2,y2),试比较y1和y2的大小:y1 y2(填“>”“<”“=”).
=1,且经过点(-1,y1)、(2,y2),试比较y1和y2的大小:y1 y2(填“>”“<”“=”).
查看答案和解析>>
科目:初中数学 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:单选题
如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是( )
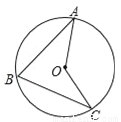
A. 150° B. 140° C. 130° D. 120°
A 【解析】试题分析:∵A、B、C是⊙O上的三点,∠B=75°,∴∠AOC=2∠B=150°.故选A.查看答案和解析>>
科目:初中数学 来源:2017年天津二十一中中考数学冲刺试卷(一) 题型:单选题
已知圆锥的底面半径为5cm,侧面积为65πcm2,设圆锥的母线与高的夹角为θ,如图所示,则sinθ的值为( )
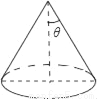
A. 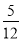 B.
B. 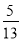 C.
C. 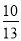 D.
D. 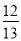
查看答案和解析>>
科目:初中数学 来源:湖南省新化县2016-2017学年度第二学期期中检测七年级数学试卷 题型:填空题
若(17x-11)(7x-3)-(7x-3)(9x-2)=(ax+b)(8x-c),其中a,b,c是整数,则a+b+c的值等于________.
13 【解析】【解析】 (17x﹣11)(7x﹣3)﹣(7x﹣3)(9x﹣2)=(7x﹣3)[(17x﹣11)﹣(9x﹣2)] =(7x﹣3)(8x﹣9) ∵(17x﹣11)(7x﹣3)﹣(7x﹣3)(9x﹣2)=(ax+b)(8x﹣c),可因式分解成(7x﹣3)(8x﹣9),∴a=7,b=﹣3,c=9,∴a+b+c=7﹣3+9=13. 故答案为:13.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com